题目内容
4.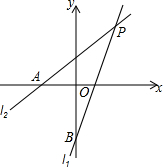 如图,在平面直角坐标系中,直线l1:y=x+1与x轴交于点A,直线l2:y=$\frac{4}{3}$x-1与y轴交于点B,并且直线l1与l2交于点P.
如图,在平面直角坐标系中,直线l1:y=x+1与x轴交于点A,直线l2:y=$\frac{4}{3}$x-1与y轴交于点B,并且直线l1与l2交于点P.(1)求出P点坐标;
(2)求∠OAP+∠APB+∠∠BPA的度数.
分析 (1)把两个函数联立方程组求得交点P的坐标即可;
(2)连接PO并延长作射线PC,利用三角形的外角的性质求得答案即可.
解答 解:(1)由题意得
$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{4}{3}x-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$,
因此P点坐标为(6,7);
(2)如图,
连接PO并延长作射线PC,
∵∠AOC=∠PAO+∠APO,∠BOC=∠PBO+∠BPO,
∴∠OAP+∠APB+∠BPA=∠PAO+∠APO+∠BPO+∠PBO=∠A0C+∠BOC=∠AOB=90°.
点评 此题考查两条直线的交点问题,三角形的外角的性质,把两个函数联立方程组即可求得两个函数的交点坐标.

练习册系列答案
相关题目
9.多项式2x3-x2y2+y3+25的次数和项数分别是( )
| A. | 5次4项 | B. | 3次4项 | C. | 4次4项 | D. | 无法确定 |
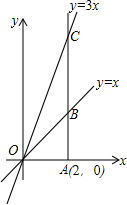 如图所示,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交与B,C两点,求三角形OBC的面积(其中O为坐标原点).
如图所示,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交与B,C两点,求三角形OBC的面积(其中O为坐标原点).