题目内容
 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.考点:平行四边形的判定,全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:根据等边三角形的性质推出∠BCE=∠FCA=60°,求出∠BCA=∠FCE,证△BCA≌△ECF,推出AD=EF=AB,同理得出DE=AF,即可得出结论.
解答:证明:∵△BCE、△ACF、△ABD都是等边三角形,
∴AB=AD,AC=CF,BC=CE,∠BCE=∠ACF,
∴∠BCE-∠ACE=∠ACF-∠ACE,
即∠BCA=∠FCE,
在△BCA和△ECF中,
,
∴△BCA≌△ECF(SAS),
∴AB=EF,
∵AB=AD,
∴AD=EF,
同理DE=AF,
∴四边形ADEF是平行四边形.
∴AB=AD,AC=CF,BC=CE,∠BCE=∠ACF,
∴∠BCE-∠ACE=∠ACF-∠ACE,
即∠BCA=∠FCE,
在△BCA和△ECF中,
|
∴△BCA≌△ECF(SAS),
∴AB=EF,
∵AB=AD,
∴AD=EF,
同理DE=AF,
∴四边形ADEF是平行四边形.
点评:此题主要考查了等边三角形的性质和平行四边形的判定.

练习册系列答案
相关题目

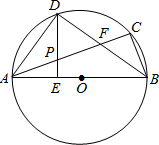 已知:如图,△ABC内接于⊙O,AB为直径.∠CBA的平分线交AC于点F,交⊙O于点D.DE⊥AB于点E,且交AC于点P.连结AD,
已知:如图,△ABC内接于⊙O,AB为直径.∠CBA的平分线交AC于点F,交⊙O于点D.DE⊥AB于点E,且交AC于点P.连结AD,