题目内容
如图是一组按照某种规律摆放的图案,第1个图中有1个三角形,第2个图中有4个三角形,第3个图中有8个三角形,则第10个图中三角形的个数是( )


| A、29 | B、28 | C、37 | D、36 |
考点:规律型:图形的变化类
专题:
分析:由图可知:第一个图案有三角形1个,第二图案有三角形1+3=4个,第三个图案有三角形1+3+4=8个,第四个图案有三角形1+3+4+4=12,…第n个图案有三角形4(n-1)个,由此得出规律解决问题.
解答:解:第一个图案有三角形1个,
第二图案有三角形1+3=4个,
第三个图案有三角形1+3+4=8个,
第四个图案有三角形1+3+4+4=12,
…
第n个图案有三角形4(n-1)个,
第10个图中三角形的个数是4×(10-1)=36.
故选:D.
第二图案有三角形1+3=4个,
第三个图案有三角形1+3+4=8个,
第四个图案有三角形1+3+4+4=12,
…
第n个图案有三角形4(n-1)个,
第10个图中三角形的个数是4×(10-1)=36.
故选:D.
点评:此题主要考查了图形的变化规律,注意由特殊到一般的分析方法.这类题型在中考中经常出现.

练习册系列答案
相关题目
a是不为1的有理数,我们把
称为a的差倒数,如:2的差倒数是
=-1,-1的差倒数是
=
,已知a1=
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2015=( )
| 1 |
| 1-a |
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
| B、-2 | ||
C、
| ||
D、-
|
对于任意实数a,b,定义a•b=a+3b,则对于函数y=x2•x+(-1)•1,当0<x<1时,y的取值范围为( )
| A、0<y<6 |
| B、2<y<6 |
| C、0≤y≤6 |
| D、2≤y≤6 |
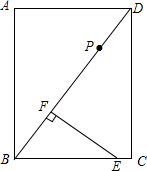 如图,在矩形ABCD中,BC=6cm,AB=8cm,E是BC上的一点,且BE=5cm,过点E作EF⊥BD,垂足为F,点P从D出发沿DB方向向点B运动,速度为1cm/秒,运动时间为t秒.在矩形边上找一点Q,使得以E,F,P,Q为顶点的四边形为平行四边形,则t值为
如图,在矩形ABCD中,BC=6cm,AB=8cm,E是BC上的一点,且BE=5cm,过点E作EF⊥BD,垂足为F,点P从D出发沿DB方向向点B运动,速度为1cm/秒,运动时间为t秒.在矩形边上找一点Q,使得以E,F,P,Q为顶点的四边形为平行四边形,则t值为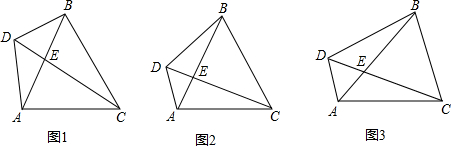
 如图所示,点C分线段AB为5:7两个部分(AC<BC),点D分AC为5:7的两个部分(AD<DC),且CD=5cm,则AB的长为
如图所示,点C分线段AB为5:7两个部分(AC<BC),点D分AC为5:7的两个部分(AD<DC),且CD=5cm,则AB的长为