题目内容
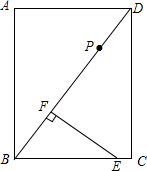 如图,在矩形ABCD中,BC=6cm,AB=8cm,E是BC上的一点,且BE=5cm,过点E作EF⊥BD,垂足为F,点P从D出发沿DB方向向点B运动,速度为1cm/秒,运动时间为t秒.在矩形边上找一点Q,使得以E,F,P,Q为顶点的四边形为平行四边形,则t值为
如图,在矩形ABCD中,BC=6cm,AB=8cm,E是BC上的一点,且BE=5cm,过点E作EF⊥BD,垂足为F,点P从D出发沿DB方向向点B运动,速度为1cm/秒,运动时间为t秒.在矩形边上找一点Q,使得以E,F,P,Q为顶点的四边形为平行四边形,则t值为考点:平行四边形的判定,矩形的性质
专题:动点型
分析:根据条件可证明△BEF∽△BDC,可求得EF,当以E,F,P,Q为顶点的四边形为平行四边形时结合条件可知PQ∥EF,且PQ=EF,再分Q在AD、AB、CD三边上分别求得PD的长,可求得t的值.
解答:解:∵BC=6cm,AB=8cm,
∴BD=10,
∵四边形ABCD为矩形,
∴∠C=∠EFB,且∠EBF=∠CBD,
∴△BEF∽△BDC,
∴
=
,即
=
,
∴EF=4cm,
当以E,F,P,Q为顶点的四边形为平行四边形时,则有PQ=EF=4cm,且PQ∥EF,
∵EF⊥BD,
∴PQ⊥BD,
∴∠QPD=90°,
设运动时间为t秒,则PD=tcm,
①当Q在AD上时,如图1,
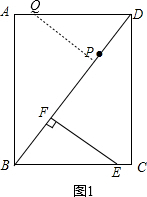
∵四边形ABCD为矩形,
∴∠A=∠QPD=90°,且∠QDP=∠BDA,
∴△QPD∽△BAD,
∴
=
,即
=
,
∴PD=4,所以t=4s,
②当Q在AB上时,如图2,
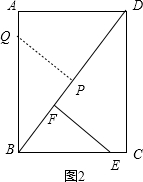
同理可得
=
,即
=
,解得PB=
,
∴PD=BD-PB=10-
=
,
∴t=
s,
③当Q在CD上时,如图3,
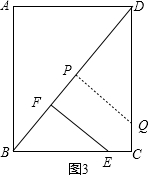
同理可得
=
,即
=
,解得PD=
,
∴t=
s,
综上可知t的值为4秒或
秒或
秒,
故答案为:4或
或
.
∴BD=10,
∵四边形ABCD为矩形,
∴∠C=∠EFB,且∠EBF=∠CBD,
∴△BEF∽△BDC,
∴
| BE |
| BD |
| EF |
| CD |
| 5 |
| 10 |
| EF |
| 8 |
∴EF=4cm,
当以E,F,P,Q为顶点的四边形为平行四边形时,则有PQ=EF=4cm,且PQ∥EF,
∵EF⊥BD,
∴PQ⊥BD,
∴∠QPD=90°,
设运动时间为t秒,则PD=tcm,
①当Q在AD上时,如图1,

∵四边形ABCD为矩形,
∴∠A=∠QPD=90°,且∠QDP=∠BDA,
∴△QPD∽△BAD,
∴
| PD |
| AD |
| PQ |
| AB |
| PD |
| 6 |
| 4 |
| 8 |
∴PD=4,所以t=4s,
②当Q在AB上时,如图2,

同理可得
| PB |
| AB |
| PQ |
| AD |
| PB |
| 8 |
| 4 |
| 6 |
| 16 |
| 3 |
∴PD=BD-PB=10-
| 16 |
| 3 |
| 14 |
| 3 |
∴t=
| 14 |
| 3 |
③当Q在CD上时,如图3,

同理可得
| PD |
| CD |
| PQ |
| BC |
| PD |
| 8 |
| 4 |
| 6 |
| 16 |
| 3 |
∴t=
| 16 |
| 3 |
综上可知t的值为4秒或
| 14 |
| 3 |
| 16 |
| 3 |
故答案为:4或
| 14 |
| 3 |
| 16 |
| 3 |
点评:本题主要考查矩形及平行四边形的性质及相似三角形的判定和性质,由条件确定出Q点所在的位置是解题的关键,注意分类讨论思想的应用.

练习册系列答案
相关题目
下面四个图形中,∠1与∠2是对顶角的图形是( )
A、 |
B、 |
C、 |
D、 |
 图中有12个1×1的小正方形,它们共有20个顶点,从中取出3个,作为三角形的顶点,问:这些三角形中,面积是2的有多少个?
图中有12个1×1的小正方形,它们共有20个顶点,从中取出3个,作为三角形的顶点,问:这些三角形中,面积是2的有多少个?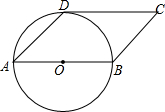 如图,四边形ABCD是平行四边形,AB=2,以边AB为直径的⊙O经过点D,且∠DAB=45°.
如图,四边形ABCD是平行四边形,AB=2,以边AB为直径的⊙O经过点D,且∠DAB=45°.