题目内容
对于任意实数a,b,定义a•b=a+3b,则对于函数y=x2•x+(-1)•1,当0<x<1时,y的取值范围为( )
| A、0<y<6 |
| B、2<y<6 |
| C、0≤y≤6 |
| D、2≤y≤6 |
考点:二次函数的性质
专题:新定义
分析:利用定义求出二次函数的表达式,再利用函数的增减性质求出当0<x<1时是增函数,代入即可求出y的取值范围.
解答:解:∵a•b=a+3b,
∴y=x2•x+(-1)•1=x2+3x+2,
∵函数的对称轴为x=-
,且开口向上,
∴当x>-
时,是增函数,
∴当0<x<1时,2<y<6.
故选:B.
∴y=x2•x+(-1)•1=x2+3x+2,
∵函数的对称轴为x=-
| 3 |
| 2 |
∴当x>-
| 3 |
| 2 |
∴当0<x<1时,2<y<6.
故选:B.
点评:本题主要考查了二次函数的性质,解题的关键是利用定义求出二次函数的表达式.

练习册系列答案
相关题目
一鞋店试销一种新款女鞋,试销期间卖出情况如表:
对于这个鞋店的经理来说最关心哪种型号的鞋畅销,则下列统计量对鞋店经理来说最有意义的是( )
| 型号 | 220 | 225 | 230 | 235 | 240 | 245 | 250 |
| 数量(双) | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
| A、平均数 | B、众数 |
| C、中位数 | D、方差 |
下列事件中,必然事件是( )
| A、掷一枚硬币,正面朝上 |
| B、a是实数,|a|≥0 |
| C、某运动员立定跳远的最好成绩是3.2米 |
| D、从车间刚生产的产品中任意抽取一个,是次品 |

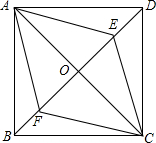 如图,在正方形ABCD中,对角线AC与BD相交于点O,点E、F在对角线BD上,且BF=DE.
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E、F在对角线BD上,且BF=DE.