题目内容
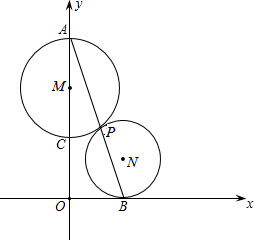 如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系,
如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系,(1)求证:OB是⊙N的切线;
(2)如果OC=CM=MA=1,圆N在始终保持与圆M外切,与x轴相切的情况下运动,设N点的坐标是(x,y),求y与x的函数的关系式.
考点:圆的综合题
专题:
分析:(1)首先作辅助线:连接MN、NB,则MN过点P,即可得:∠MAP=∠MPA=∠NPM=∠NBP,则可证得:NB∥AO,又由A0⊥OB,证得:NB⊥OB,则问题得证;
(2)作ND⊥y轴,在Rt△MDN中,利用勾股定理即可求得y与x之间的函数关系式.
(2)作ND⊥y轴,在Rt△MDN中,利用勾股定理即可求得y与x之间的函数关系式.
解答:(1)证明:连接MN、NB,则MN过点P,
∵MA=MN,MQ=NB,
∴∠MAP=∠MPA=∠NPM=∠NBP,
∴NB∥AO,
又A0⊥OB,
∴NB⊥OB.
又NB是半径,
∴OB是⊙N的切线.
(2)解:作ND⊥y轴,垂足为D.
则MD=|2-y|,ND=|x|,MN=|1+y|,
在Rt△MDN中,MD2+DN2=MN2,
∴|2-y|2+|x|2=|1+y|2,
∴y=
x2+
.
∵MA=MN,MQ=NB,

∴∠MAP=∠MPA=∠NPM=∠NBP,
∴NB∥AO,
又A0⊥OB,
∴NB⊥OB.
又NB是半径,
∴OB是⊙N的切线.
(2)解:作ND⊥y轴,垂足为D.
则MD=|2-y|,ND=|x|,MN=|1+y|,
在Rt△MDN中,MD2+DN2=MN2,
∴|2-y|2+|x|2=|1+y|2,
∴y=
| 1 |
| 6 |
| 1 |
| 2 |
点评:此题考查了圆的性质,切线的判定以及勾股定理的运用等知识.此题综合性很强,图形也很复杂,解题的关键是注意数形结合思想的应用与辅助线的添加方法.

练习册系列答案
相关题目
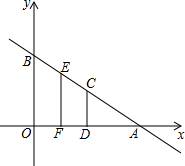 如图,平面直角坐标系中,直线AB解析式为:y=
如图,平面直角坐标系中,直线AB解析式为:y= a、b、c三个数在数轴上位置如图所示,且丨a丨=丨c丨,化简丨a丨-丨b+a丨+丨b-c丨+c+丨c+a丨=
a、b、c三个数在数轴上位置如图所示,且丨a丨=丨c丨,化简丨a丨-丨b+a丨+丨b-c丨+c+丨c+a丨=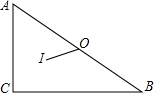 如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长. 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是