题目内容
若方程x2-3x-k=0无实数解，则k的取值范围是 ．
考点：根的判别式
专题：
分析：先求出△的值，再根据方程无实数根求出k的取值范围即可．
解答：解：∵方程x2-3x-k=0无实数解，
∴△＜0，△=9+4k＜0，解得k＜-
．
故答案为：k＜-
．
∴△＜0，△=9+4k＜0，解得k＜-
| 9 |
| 4 |
故答案为：k＜-
| 9 |
| 4 |
点评：本题考查的是根的判别式，熟知一元二次方程ax2+bx+c=0（a≠0）的根与△的关系是解答此题的关键．
练习册系列答案
相关题目
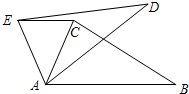如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△ADE的位置，连接EC，满足EC∥AB，则∠BAD的度数为（ ）| A、30° | B、35° |
| C、40° | D、50° |
下列说法中不正确的是（ ）
| A、经过平移，图形对应点连成的线段平行且相等 |
| B、平移中，图形上每个点移动的距离不同 |
| C、经过平移，图形的对应线段，对应角分别相等 |
| D、平移不改变图形的形状和大小 |
已知
是方程mx+2y=2的一个解，那么m为（ ）
|
| A、4 | ||
B、
| ||
| C、-4 | ||
| D、1 |
一次函数y=kx+b（k、b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x的方程kx+b+1=0的解为