题目内容
2.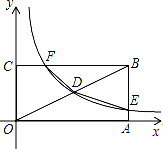 如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )
如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
分析 据反比例函数图象上点的坐标特征设D点坐标为(a,$\frac{k}{a}$),由点D为对角线OB的中点,可得B(2a,$\frac{2k}{a}$),再分别表示出E(2a,$\frac{k}{2a}$),F($\frac{a}{2}$,$\frac{2k}{a}$),利用四边形BEDF的面积=S△DBF+S△BED得到$\frac{1}{2}$(2a-$\frac{a}{2}$)•($\frac{2k}{a}$-$\frac{k}{a}$)+$\frac{1}{2}$(2a-a)•($\frac{2k}{a}$-$\frac{k}{2a}$)=4.5,然后解方程即可得到k的值.
解答 解:设D点坐标为(a,$\frac{k}{a}$),
∵点D为对角线OB的中点,
∴B(2a,$\frac{2k}{a}$),
∵四边形ABCO为矩形,
∴E点的横坐标为2a,F点的纵坐标$\frac{2k}{a}$,
∴E(2a,$\frac{k}{2a}$),F($\frac{a}{2}$,$\frac{2k}{a}$),
∵四边形BEDF的面积=S△DBF+S△BED,
∴$\frac{1}{2}$(2a-$\frac{a}{2}$)•($\frac{2k}{a}$-$\frac{k}{a}$)+$\frac{1}{2}$(2a-a)•($\frac{2k}{a}$-$\frac{k}{2a}$)=4.5,
∴k=3.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知正n边形的一个内角为135°,则边数n的值是( )
| A. | 10 | B. | 8 | C. | 7 | D. | 6 |
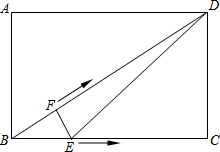 已知,如图,在矩形ABCD中,AB=6cm,BC=8cm,动点E、F同时从B点出发,点E沿射线BC方向以5cm/s运动,点F沿线段BD方向以4cm/s运动,当点F到达D时,运动停止,连接DE,设运动时间为t(s).
已知,如图,在矩形ABCD中,AB=6cm,BC=8cm,动点E、F同时从B点出发,点E沿射线BC方向以5cm/s运动,点F沿线段BD方向以4cm/s运动,当点F到达D时,运动停止,连接DE,设运动时间为t(s).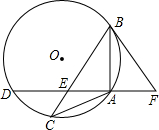 如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE. 如图,在△ABC中,∠C=90°.
如图,在△ABC中,∠C=90°.