题目内容
17.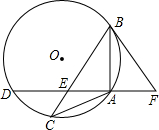 如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.(1)试判断BF与⊙O的位置关系,并说明理由;
(2)若BF=5,cos∠C=$\frac{4}{5}$,求⊙O的直径;
(3)若cos∠F=$\frac{3}{5}$,则$\frac{{{S_{△ACE}}}}{{{S_{△ABE}}}}$=$\frac{7}{25}$.(直接填写结果)
分析 (1)连接OB、OA或连接BD,由于AB=AC,则∠ABC=∠C,由AF=AE,则∠EBA=∠FBA,从而得出∠ABD+∠FBA=90°,即OB⊥BF,则BF是⊙O切线;
(2)由(1)得∠C=∠D,再由cos∠D=$\frac{4}{5}$,得$\frac{BD}{DF}$=$\frac{4}{5}$、$\frac{BF}{DF}$=$\frac{3}{5}$,从而求出BD.
(3)根据两三角形的高相同,它们的面积的比等于底边的比求解即可.
解答 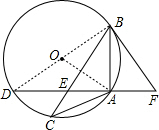 证明:(1)BF与⊙O相切,连接OB、OA,连接BD,
证明:(1)BF与⊙O相切,连接OB、OA,连接BD,
∵AD⊥AB,∴∠BAD=90°
∴BD是直径,∴BD过圆心
∵AB=AC,
∴∠ABC=∠C,
∵∠C=∠D,
∴∠ABC=∠D,
∵AD⊥AB,
∴∠ABD+∠D=90°,
∵AF=AE,
∴∠EBA=∠FBA,
∴∠ABD+∠FBA=90°,
∴OB⊥BF,
∴BF是⊙O切线(4分);
(2)∵∠C=∠D,cos∠C=$\frac{4}{5}$,
∴cos∠D=$\frac{4}{5}$,
∵BF=5,
∴$\frac{BD}{DF}$=$\frac{4}{5}$,
∴$\frac{BF}{DF}$=$\frac{3}{5}$,
∴BD=$\frac{4}{3}$×5=$\frac{20}{3}$,
∴直径为$\frac{20}{3}$;
(3)∵cos∠F=$\frac{3}{5}$,
∴cos∠BEA=$\frac{3}{5}$,
设AF=AE=3x,则BF=BE=5x、AB=AC=4x,
∴BD=$\frac{20}{3}x$,AD=$\frac{16x}{3}$,
∴DE=$\frac{7}{3}$x,
∵△ACE∽△BDE,
∴CE:DE=AE:BE,
∴CE=$\frac{7}{5}$x,
∴$\frac{{{S_{△ACE}}}}{{{S_{△ABE}}}}$=$\frac{CE}{BE}$=$\frac{\frac{7}{5}x}{5}$=$\frac{7}{25}$.
点评 此题考查了切线的判定方法相似三角形的判定级性质及圆的综合知识,运用了三角函数求线段的长,综合性较强,难度偏大.

 精英口算卡系列答案
精英口算卡系列答案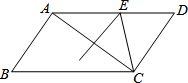 如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )
如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )| A. | 14 | B. | 20 | C. | 22 | D. | 24 |
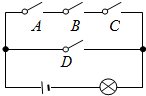 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{5}$ |
| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | -4 |
 菱形ABCD中,对角线AC,BD交于点O,BE⊥AD交AC于F,AF=BD,G为BD上的点,EG∥AB.
菱形ABCD中,对角线AC,BD交于点O,BE⊥AD交AC于F,AF=BD,G为BD上的点,EG∥AB.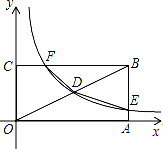 如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )
如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )