题目内容
12.已知关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2,当x12-x22=0时,则m的值为$\frac{1}{4}$.分析 由x12-x22=0得x1+x2=0或x1-x2=0;当x1+x2=0时,运用两根关系可以得到-2m-1=0或方程有两个相等的实根,据此即可求得m的值.
解答 解:由两根关系,得根x1+x2=-(2m-1),x1•x2=m2,
由x12-x22=0得(x1+x2)(x1-x2)=0,
若x1+x2=0,即-(2m-1)=0,解得m=$\frac{1}{2}$,
∵$\frac{1}{2}$>$\frac{1}{4}$,
∴m=$\frac{1}{2}$不合题意,舍去,
若x1-x2=0,即x1=x2
∴△=0,由(1)知$\frac{1}{4}$,
故当x12-x22=0时,m=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了一元二次方程根的判别式及根与系数关系,利用两根关系得出的结果必须满足△≥0的条件.

练习册系列答案
相关题目
2.在等式y=kx+b中,当x=2时,y=2;当x=0时,y=4,则当x=-2时,y的值是( )
| A. | -10 | B. | -8 | C. | 6 | D. | 4 |
7.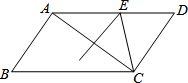 如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )
如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )
 如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )
如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )| A. | 14 | B. | 20 | C. | 22 | D. | 24 |
17.下列运算正确的是( )
| A. | 2x2+x=3x3 | B. | (-x)3+x2=-x6 | C. | (2x2)3=6x6 | D. | (-x)2÷x=x |
 今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某数学兴趣小组在本校学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题.
今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某数学兴趣小组在本校学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题.
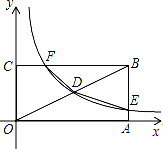 如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )
如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )