题目内容

13．小明在计算一个多边形的内角和时，由于多加了一个外角，得到的答案为1665°，你能找出多边形的这个外角的度数及这个多边形的边数吗？

分析 根据多边形的内角和公式（n-2）•180°可知，多边形的内角和是180°的倍数，然后求出多边形的边数以及多加的外角的度数即可得解．

解答 解：设多边形的边数为n，多加的外角度数为α，则
（n-2）•180°=1665°-α，
∵1665°=9×180°+45°，内角和应是180°的倍数，
∴同学多加的一个外角为45°，
∴这是9+2=11边形的内角和，
这个多边形一定有一个内角是180°-45°=135°．
答：他计算的是11边形的内角和，这个多边形一定有一个内角是135°．

点评 本题考查了多边形的内角和公式，根据多边形的内角和公式判断出多边形的内角和公式是180°的倍数是解题的关键．

练习册系列答案
相关题目
3．今年以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点．为了调查学生对雾霾天气知识的了解程度，某数学兴趣小组在本校学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查结果，绘制了如图的统计图，结合统计图，回答下列问题．
（1）本次抽样调查的样本容量是400；
（2）若该校有学生1500人，请根据调查结果估计这些学生中“比较了解”雾霾天气知识的人数约为多少？
（3）根据调查结果，学校准备开展关于雾霾天气知识竞赛，某班要从“非常了解”的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：在一个不透明的袋中装有2个红球和2个白球，它们除了颜色外无其它差别，从中随机摸出两个球，若摸出的两个球颜色相同，则小明去；否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．
4．为了解中考体育科目训练情况，改进训练方法，减轻学生负担，某县教育局从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如图两幅不完整的统计图．
请根据统计图中的信息解答下列问题：
（1）本次抽样测试的学生人数是40；
（2）图中∠α的度数是54°，并把图2条形统计图补充完整；
（3）全县九年级共有学生8500名，如果全部参加这次中考体育科目测试，请估计不及格的人数为1700．
1．二元一次方程组$\left\{\begin{array}{l}{x+2y=3}\\{2x-y=1}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$．
8．菱形ABCD中，对角线AC，BD交于点O，BE⊥AD交AC于F，AF=BD，G为BD上的点，EG∥AB．
（1）求证：△AEF≌△BED；
（2）求证：BO=（$\sqrt{2}$+1）OG．
18．用半径为3，圆心角为120°的扇形围成一个圆锥的侧面，则这个圆锥的全面积为4π．
5．小明在学习反比例函数的图象时，他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤，在纸上逐步探索函数y2=$\frac{2}{x}$的图象，并且在黑板上写出4个点的坐标：A$（\;\frac{3}{2}，\frac{4}{3}\;）$，B（1，2），C$（\;1，\;\frac{1}{2}\;）$，D（-2，-1）．
（1）在A、B、C、D四个点中，任取一个点，这个点既在直线y1=x+1又在双曲线y2=$\frac{2}{x}$上的概率是多少？
（2）小明从A、B、C、D四个点中任取两个点进行描点，求两点都落在双曲线y2=$\frac{2}{x}$上的概率．
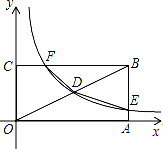2．如图，矩形OABC的顶点A、C分别在x、y的正半轴上，点D为对角线OB的中点，反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D，且与AB、BC分别交于E、F两点，若四边形BEDF的面积为4.5，则k的值为（　　）
A．2B．3C．6D．4

已知：如图(1)，直线AB∥CD，EF分别交AB、CD于E、F两点，∠BEF、∠DFE的平分线相交于点K．（1）求∠EKF的度数．（计算过程不准用三角形内角和）（2）如图(2)，∠BEK、∠DFK的平分线相交于点K1，问∠K1与∠K的度数是否存在某种特定的等量关系？写出结论并证明．（3）在图2中作∠BEK1、∠DFK1的平分线相交于点K2，作∠BEK2、∠DFK2的平分线相交于点K3，依此类推，作∠BEKn、∠DFKn的平分线相交于点Kn+1，请用含的n式子表示∠Kn+1的度数．（直接写出答案，不必写解答过程）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网