题目内容
16.已知关于x的方程3a+x=$\frac{ax}{2}$+3的解为x=4,则a-2a+3a-4a+5a-6a+…+99a-100a的值为50.分析 根据方程的解满足方程,可得关于a的方程,根据解方程,可得a的值,根据代数式求值,可得答案.
解答 解:将x=4代入3a+x=$\frac{ax}{2}$+3,得
3a+4=2a+3,
解得a=-1.
a-2a+3a-4a+5a-6a+…+99a-100a=(a-2a)+(3a-4a)+(5a-6a)+…+(99a-100a)
=$\stackrel{50}{\overbrace{-a+(-a)+…+(-a)+(-a)}}$=50(-a)
当a=-1时,原式=-50×(-1)=50,
故答案为:50.
点评 本题考查了一元一次方程的解,利用方程的解满足方程得出a的值是解题关键,又利用了加法结合律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.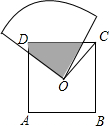 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )
 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )| A. | $\frac{1}{3}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{1}{2}$a2 | D. | $\frac{1}{4}$a |
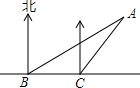 如图,海中有一小岛.它周围20海里内有暗礁.一货船由西向东航行.在B点测得岛A在北偏东65°的方向上,航行30海里到达C点.这时小岛A在北偏东40°处.如果货船不改变方向.继续向东航行,有没有触礁的危险?并说明理由.(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.19).
如图,海中有一小岛.它周围20海里内有暗礁.一货船由西向东航行.在B点测得岛A在北偏东65°的方向上,航行30海里到达C点.这时小岛A在北偏东40°处.如果货船不改变方向.继续向东航行,有没有触礁的危险?并说明理由.(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.19).