题目内容
9.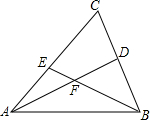 如图所示,在△ABC中,AD是BC边的中线,F是AD的中点,连接BF并延长交AC于E,求证:EC=2AE.
如图所示,在△ABC中,AD是BC边的中线,F是AD的中点,连接BF并延长交AC于E,求证:EC=2AE.
分析 过E作DG∥AC交BE于点G,则DG是△BEC的中位线,利用中位线定理即可证得.
解答  证明:∵AD是BC边的中线,F是AD的中点,
证明:∵AD是BC边的中线,F是AD的中点,
∴点D是BC的中点,DF=AF.
如图,过E作DG∥AC交BE于点G.
∵DG∥AC,且AD是BC边的中线.
∴DG是△BEC的中位线,△DGF∽△AEF,
∴DG=$\frac{1}{2}$EC,$\frac{DG}{AE}$=$\frac{DF}{AF}$=1
∴DG=AE,
∴AE=$\frac{1}{2}$EC.
即EC=2AE.
点评 此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.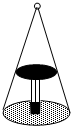 如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )
如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )
 如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )
如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )| A. | 0.36π米2 | B. | 0.81π米2 | C. | 2π米2 | D. | 3.24π米2 |
19.已知等腰三角形的两内角的度数之比为1:4,则顶角为( )度.
| A. | 20 | B. | 120 | C. | 20或120 | D. | 36 |