题目内容
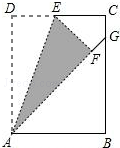 如图,在矩形ABCD中,点E是边CD的中点,AB=2,AD=3,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部,将AF延长交边BC于点C,则CG的长为
如图,在矩形ABCD中,点E是边CD的中点,AB=2,AD=3,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部,将AF延长交边BC于点C,则CG的长为考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线,首先证明△EFG≌△ECG,得到FG=CG(设为x ),∠FEG=∠CEG;同理可证AF=AD=3,∠FEA=∠DEA,进而证明△AEG为直角三角形,运用射影定理即可解决问题.
解答: 解:如图,连接EG;
解:如图,连接EG;
∵四边形ABCD为矩形,
∴∠D=∠C=90°,DC=AB=2;
由题意得:EF=DE=EC=1,∠EFG=∠D=90°;
在Rt△EFG与Rt△ECG中,
,
∴△EFG≌△ECG,
∴FG=CG(设为x ),∠FEG=∠CEG;
同理可证:AF=AD=3,∠FEA=∠DEA,
∴∠AEG=
×180°=90°,
而EF⊥AG,由射影定理得:
12=3•x,
∴x=
,
即CG的长为
,
故该题答案为
.
 解:如图,连接EG;
解:如图,连接EG;∵四边形ABCD为矩形,
∴∠D=∠C=90°,DC=AB=2;
由题意得:EF=DE=EC=1,∠EFG=∠D=90°;
在Rt△EFG与Rt△ECG中,
|
∴△EFG≌△ECG,
∴FG=CG(设为x ),∠FEG=∠CEG;
同理可证:AF=AD=3,∠FEA=∠DEA,
∴∠AEG=
| 1 |
| 2 |
而EF⊥AG,由射影定理得:
12=3•x,
∴x=
| 1 |
| 3 |
即CG的长为
| 1 |
| 3 |
故该题答案为
| 1 |
| 3 |
点评:该题以矩形为载体,以翻折变换为方法,以考查全等三角形的性质及其应用、射影定理等几何知识点为核心构造而成;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
如图所示,不可能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
X<0,Y>0时,则X,X+Y,X-Y,Y中最小的数是( )
| A、X-Y | B、Y | C、X+Y | D、X |
下列说法:
①角平分线上的点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等;
④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中,所有正确说法的序号是( )
①角平分线上的点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等;
④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中,所有正确说法的序号是( )
| A、①②③ | B、②③④ |
| C、①③ | D、②④ |
 如图所示,在Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC与△BDC相似,求CD的长.
如图所示,在Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC与△BDC相似,求CD的长. 如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( )
如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( )