题目内容
 如图,P是直线y=-x+4上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与x轴相切,点P的坐标为
如图,P是直线y=-x+4上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与x轴相切,点P的坐标为考点:切线的性质,一次函数图象上点的坐标特征
专题:计算题
分析:根据切线的性质得到点P到x轴的距离为1,则点P的纵坐标为1或-1,然后根据一次函数图象上点的坐标特征确定P点坐标.
解答:解:∵当⊙P与x轴相切,而⊙P的半径为1,
∴点P到x轴的距离为1,
∴点P的纵坐标为1或-1,
当x=1时,y=-x+4=-1+4=3,此时P点坐标为(3,1);
当x=-1时,y=-x+4=1+4=5,此时P点坐标为(5,-1).
∴满足条件的P点坐标为(3,1)或(5,-1).
故答案为(3,1)或(5,-1).
∴点P到x轴的距离为1,
∴点P的纵坐标为1或-1,
当x=1时,y=-x+4=-1+4=3,此时P点坐标为(3,1);
当x=-1时,y=-x+4=1+4=5,此时P点坐标为(5,-1).
∴满足条件的P点坐标为(3,1)或(5,-1).
故答案为(3,1)或(5,-1).
点评:本题考查了切线的性质:圆心到切线的距离等于圆的半径.也考查了坐标与图形性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列比较大小正确的是( )
A、-
| ||||
| B、π-4<-2 | ||||
| C、-(-2)3<0 | ||||
| D、-2<-5 |
如图所示,不可能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
已知x:y=5:2,则下列各式中不正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
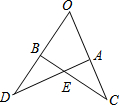 如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )
如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )| A、130° | B、85° |
| C、105° | D、95° |

 将图中的硬纸盘按虚线折叠,可以围成怎样的几何体.
将图中的硬纸盘按虚线折叠,可以围成怎样的几何体. 如图所示,在Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC与△BDC相似,求CD的长.
如图所示,在Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC与△BDC相似,求CD的长.