题目内容
15．贵阳市甲、乙两个大数据呼叫中心联合组织一次技能比赛，两个中心分别选出1男2女共6名接线员参加比赛．（1）若从两个中心所有参加比赛人员中随机选1名，求所选的接线员性别为女性的概率；
（2）若从参赛的6名人员中随机选2名，用列表法或画树状图的方法求这2名接线员来自不同呼叫中心的概率．
分析 （1）根据概率公式直接计算即可；
（2）设甲市中1男2女代号分别为1，2，3；乙市1男2女分别为4，5，6，列出树形图即可求出这2名接线员来自不同呼叫中心的概率．
解答 解：（1）
∵两个中心分别选出1男2女共6名接线员参加比赛，
∴所有参加比赛人员中随机选1名，所选的接线员性别为女性的概率=$\frac{4}{6}$=$\frac{2}{3}$；
（2）列表如下：
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） | |
| 2 | （2，1） | （2，3） | （2，4） | （2，5） | （2，6） | |
| 3 | （3，1） | （3，2） | （3，4） | （3，5） | （3，6） | |
| 4 | （4，1） | （4，2） | （4，3） | （4，5） | （4，6） | |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，6） | |
| 6 | （6，1） | （6，2） | （6，3） | （6，4） | （6，5） |
所以2名接线员来自不同呼叫中心的概率=$\frac{18}{30}$=$\frac{3}{5}$．
点评 本题考查了用列表与树状图求概率问题；用到的知识点为：概率=所求情况数与总情况数之比；得到所求的情况数是解决本题的关键．
练习册系列答案
提分百分百检测卷系列答案
相关题目
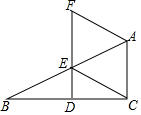如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DE，连接CE、AF．
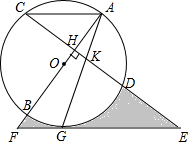如图，AB是⊙O的直径，弦CD⊥AB于H，G为⊙O上一点，AG交CD于K，E为CD延长线上一点，且EK=EG，EG的延长线交AB的延长线于F．
10．若等腰三角形的一边是9，另一边是4，则此等腰三角形的周长是（ ）
| A． | 22 | B． | 17 | C． | 22或17 | D． | 无法确定 |
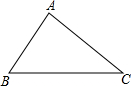如图，在△ABC中，∠B=55°，∠C=40°，直线MN垂直平分AC，交BC于点D，连接AD．