题目内容
1.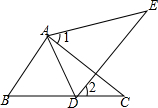 如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.
如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.
分析 根据∠1=∠2结合三角形内角和定理可得∠E=∠C,再有条件AE=AC,添加BC=DE可利用SAS定理判定△ABC≌△ADE.
解答 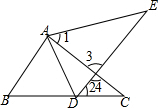 解:选②BC=DE,
解:选②BC=DE,
∵∠1=∠2,∠3=∠4,
∴∠E=∠C,
在△ADE和△ABC中,$\left\{\begin{array}{l}{AE=AC}\\{∠E=∠C}\\{DE=BC}\end{array}\right.$,
∴△ABC≌△ADE(SAS).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
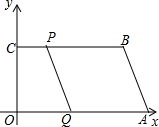 已知,点A(10,0),C(0,3),B(6,3),动点P、Q分别从C、A两点同时出发,点P以每秒1个单位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5).
已知,点A(10,0),C(0,3),B(6,3),动点P、Q分别从C、A两点同时出发,点P以每秒1个单位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5).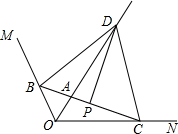 如图,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D,∠MON=130°,则∠BDC=( )
如图,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D,∠MON=130°,则∠BDC=( )