题目内容
12.随着人们生活水平的不断提高,某市私家车拥有量逐年增加,据统计,某小区2011年年底拥有家庭轿车64辆,2013年年底家庭轿车拥有量达到100辆.(1)若该小区2011年年底到2013年年底家庭轿车拥有量的年平均增长率相同,按照这个增长速度,求该小区到2014年年底家庭轿车拥有量将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投15万元,再建若干个停车位,据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划建造露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区建设两种车位的所有方案.
分析 (1)增长率的问题,用解增长率问题的模型解答;
(2)根据两种车位数量是未知数,建立等式和不等式两种关系,而车位数为整数,变无数解为有限解.
解答 解:(1)设家庭轿车拥有量的年平均增长率为x,
则64(1+x)2=100
解得x=$\frac{1}{4}$=25%,或x=-$\frac{9}{4}$(不合题意,舍去)
∴100(1+25%)=125
答:该小区到2014年底家庭轿车将达到125辆;
(2)设该小区可建室内车位a个,露天车位b个,
则$\left\{\begin{array}{l}{0.5a+0.1b=15}\\{2a≤b≤2.5a}\end{array}\right.$,
由①得b=150-5a
代入②得20≤a≤$\frac{150}{7}$,
∵a是正整数
∴a=20或21
当a=20时b=50,当a=21时b=45.
∴方案一:建室内车位20个,露天车位50个;
方案二:室内车位21个,露天车位45个.
点评 考查了一元二次方程的应用及一元一次不等式组的应用,解答综合题,需要由浅入深,认真读题,理解题意,合理设未知数,分步解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列说法正确的有( )
(1)有理数的绝对值一定比0大;
(2)有理数的相反数一定比0小;
(3)如果两个数的绝对值相等,那么这两个数相等;
(4)互为相反数的两个数的绝对值相等.
(1)有理数的绝对值一定比0大;
(2)有理数的相反数一定比0小;
(3)如果两个数的绝对值相等,那么这两个数相等;
(4)互为相反数的两个数的绝对值相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.用配方法解方程x2+6x+1=0,配方后的方程是( )
| A. | (x+3)2=8 | B. | (x-3)2=8 | C. | (x-3)2=10 | D. | (x+3)2=10 |
17.不能判定两个三角形全等的是( )
| A. | 三条边对应相等 | B. | 两条边及其夹角对应相等 | ||
| C. | 两角和一条边对应相等 | D. | 两条边和一条边所对的角对应相等 |
2.已知二次函数y=ax2+bx+c,函数y与自变量x的部分对应值如下表:
则当y>-1时,x的取值范围是-2<x<2.
| x | … | -4 | -2 | 0 | 2 | 4 | … |
| y | … | -4 | -1 | 0 | -1 | -4 | … |
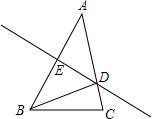 在△ABC中,DE垂直平分线段AB,交AB于E,交AC于D,已知AC=16,△BCD的周长为25,则BC=9.
在△ABC中,DE垂直平分线段AB,交AB于E,交AC于D,已知AC=16,△BCD的周长为25,则BC=9.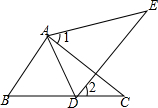 如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.
如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.