题目内容
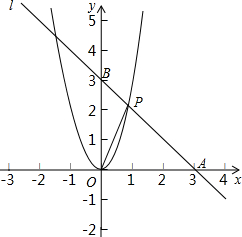 如图,直线l过A(3,0)和B(0,3)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若△AOP的面积为3,求二次函数的表达式.
如图,直线l过A(3,0)和B(0,3)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若△AOP的面积为3,求二次函数的表达式.考点:待定系数法求二次函数解析式
专题:计算题
分析:先利用待定系数法求出直线AB的解析式为y=-x+3,则可设P(t,-t+3)(0<t<3),再根据三角形面积公式得到以
•3•(-t+3)=3,解出t的值,确定P点坐标,然后把P点坐标代入y=ax2中求出a的值即可.
| 1 |
| 2 |
解答:解:设直线AB的解析式为y=kx+b,
把A(3,0),B(0,3)代入得
,解得
,
所以直线AB的解析式为y=-x+3,
设P(t,-t+3)(0<t<3),
因为△AOP的面积为3,
所以
•3•(-t+3)=3,解得t=1,
所以P点坐标为(1,2),
把P(1,2)代入y=ax2得a=2,
所以二次函数解析式为y=2x2.
把A(3,0),B(0,3)代入得
|
|
所以直线AB的解析式为y=-x+3,
设P(t,-t+3)(0<t<3),
因为△AOP的面积为3,
所以
| 1 |
| 2 |
所以P点坐标为(1,2),
把P(1,2)代入y=ax2得a=2,
所以二次函数解析式为y=2x2.
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
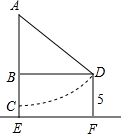 华夏古诗词源远流长,有许多古诗词与勾股定理有紧密联系,下面是明朝大数学家程大位所著的《直指算法统宗》里的一道题:
华夏古诗词源远流长,有许多古诗词与勾股定理有紧密联系,下面是明朝大数学家程大位所著的《直指算法统宗》里的一道题: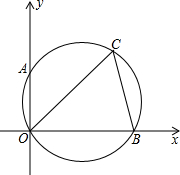 如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标.
如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标.
 如图,△ABC沿DE折叠后,点A落在BC边上的点A′处,且DE∥BC,∠B=50°,则∠BDA′=
如图,△ABC沿DE折叠后,点A落在BC边上的点A′处,且DE∥BC,∠B=50°,则∠BDA′=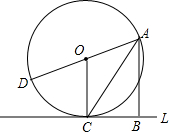 如图所示,直线L切⊙O于点C,AD为⊙O的任意一条直径,点B在直线L上,且∠BAC=∠CAD(AD与AB不在一条直线上),试判断四边形ABCO为怎样的特殊四边形?
如图所示,直线L切⊙O于点C,AD为⊙O的任意一条直径,点B在直线L上,且∠BAC=∠CAD(AD与AB不在一条直线上),试判断四边形ABCO为怎样的特殊四边形?