题目内容
1.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=-3m+2}\\{x+2y=4}\end{array}\right.$的解满足x+y>-$\frac{3}{2}$,求出满足条件的m的所有正整数值.分析 方程组两方程相加表示出x+y,代入已知不等式求出m的范围,确定出正整数值即可.
解答 解:$\left\{\begin{array}{l}{2x+y=-3m+2①}\\{x+2y=4②}\end{array}\right.$,
①+②得:3(x+y)=-3m+6,即x+y=-m+2,
代入不等式得:-m+2>-$\frac{3}{2}$,
解得:m<$\frac{7}{2}$,
则满足条件m的正整数值为1,2,3.
点评 此题考查了二元一次方程组的解,以及一元一次不等式的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
12.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
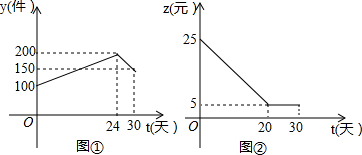

| A. | 第24天的销售量为200件 | |
| B. | 第10天销售一件产品的利润是15元 | |
| C. | 第12天与第30天这两天的日销售利润相等 | |
| D. | 第30天的日销售利润是750元 |
6.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | (-a2b)3=-a6b3 | C. | a2•a3=a6 | D. | a8÷a2=a4 |
13.观察下列关于x的单项式,探究其规律:
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是( )
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是( )
| A. | 2015x2015 | B. | 4029x2014 | C. | 4029x2015 | D. | 4031x2015 |
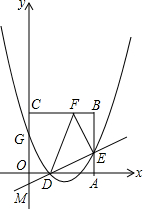 如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E.
如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E. 如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.
如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.