题目内容
5.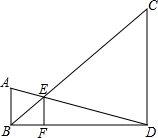 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 易证△DEF∽△DAB,△BEF∽△BCD,根据相似三角形的性质可得$\frac{EF}{AB}$=$\frac{DF}{DB}$,$\frac{EF}{CD}$=$\frac{BF}{BD}$,从而可得$\frac{EF}{AB}$+$\frac{EF}{CD}$=$\frac{DF}{DB}$+$\frac{BF}{BD}$=1.然后把AB=1,CD=3代入即可求出EF的值.
解答 解:∵AB、CD、EF都与BD垂直,
∴AB∥CD∥EF,
∴△DEF∽△DAB,△BEF∽△BCD,
∴$\frac{EF}{AB}$=$\frac{DF}{DB}$,$\frac{EF}{CD}$=$\frac{BF}{BD}$,
∴$\frac{EF}{AB}$+$\frac{EF}{CD}$=$\frac{DF}{DB}$+$\frac{BF}{BD}$=$\frac{BD}{BD}$=1.
∵AB=1,CD=3,
∴$\frac{EF}{1}$+$\frac{EF}{3}$=1,
∴EF=$\frac{3}{4}$.
故选C.
点评 本题主要考查的是相似三角形的判定与性质,发现$\frac{DF}{DB}$+$\frac{BF}{BD}$=1是解决本题的关键.

练习册系列答案
相关题目
15.长沙红星大市场某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
| A. | 562.5元 | B. | 875元 | C. | 550元 | D. | 750元 |
13.观察下列关于x的单项式,探究其规律:
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是( )
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是( )
| A. | 2015x2015 | B. | 4029x2014 | C. | 4029x2015 | D. | 4031x2015 |
20.已知∠α=35°,那么∠α的余角等于( )
| A. | 35° | B. | 55° | C. | 65° | D. | 145° |
17.下列4个数:$\sqrt{9}$、$\frac{22}{7}$、π、($\sqrt{3}$)0,其中无理数是( )
| A. | $\sqrt{9}$ | B. | $\frac{22}{7}$ | C. | π | D. | ($\sqrt{3}$)0 |
14.下列运算结果为a6的是( )
| A. | a2+a3 | B. | a2•a3 | C. | (-a2)3 | D. | a8÷a2 |
 观察如图,对照图象,请回答下列问题:
观察如图,对照图象,请回答下列问题: