题目内容
16.已知菱形的一条对角线长为a,另一条对角线为它的$\sqrt{3}$倍,用表达式表示出菱形的面积S与对角线a的函数关系S=$\frac{\sqrt{3}}{2}$a2.分析 首先表示出另一条对角线为$\sqrt{3}$a,然后根据菱形的面积等于两对角线乘积的一半列式即可求解.
解答 解:由题意,得S=$\frac{1}{2}$a•$\sqrt{3}$a=$\frac{\sqrt{3}}{2}$a2,
即菱形的面积S与对角线a的函数关系式为S=$\frac{\sqrt{3}}{2}$a2.
故答案为S=$\frac{\sqrt{3}}{2}$a2.
点评 本题考查的是菱形的性质,熟知菱形的面积等于两对角线乘积的一半是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列说法正确的有个数( )
(1)若x2=16,那么x=4
(2)$\frac{x+1}{x-1}$的倒数是$\frac{x-1}{x+1}$.
(3)两个有理数相乘,同号得正,异号得负
(4)单项式-$\frac{2ab}{3}$的系数是-$\frac{2}{3}$,次数是2.
(1)若x2=16,那么x=4
(2)$\frac{x+1}{x-1}$的倒数是$\frac{x-1}{x+1}$.
(3)两个有理数相乘,同号得正,异号得负
(4)单项式-$\frac{2ab}{3}$的系数是-$\frac{2}{3}$,次数是2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.半径为3的圆,如果半径增加2x,则面积S与x之间的函数表达式为( )
| A. | S=2π(x+3)2 | B. | S=9π+x | C. | S=4πx2+12x+9 | D. | S=4πx2+12πx+9π |
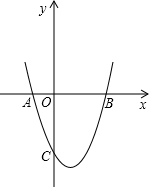 如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.
如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.