题目内容
11.菱形的两个邻角之比为2:3,周长为4a,则较短的对角线的长为2a•sinn36°.分析 根据菱形的性质在Rt△ABO中,求出AB,∠ABO,根据OA=AB•tan∠ABO即可计算.
解答 解:如图在菱形ABCD中,∠ABC:∠BCD=2:3,周长为4a,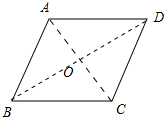
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=a,BD⊥AC,∠ABD=∠CBD,OA=OC,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠ABC=72°,
∴∠ABO=$\frac{1}{2}$∠ABC=36°,
在Rt△ABO中,AO=AB•sin∠ABO=a•sinn36°,
∴较短的对角线AC=2AO=2a•sinn36°.
故答案为2a•sin36°.
点评 本题考查菱形的性质、锐角三角函数等知识,解题的关键是熟练掌握这些知识的应用,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )
如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )
 如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )
如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 63° |
 如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.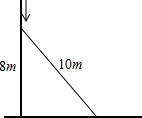 一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.
一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.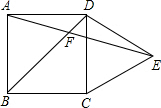 如图,在正方形ABCD外侧作等边△CDE,AE,BD相交于点F,则∠AFB=60°.
如图,在正方形ABCD外侧作等边△CDE,AE,BD相交于点F,则∠AFB=60°.