题目内容
已知在△ABC中,sinA=
,cosB=
,且AC=10cm,求△ABC的面积.
| ||
| 2 |
| ||
| 2 |
考点:解直角三角形
专题:
分析:过点C作CD⊥AB于点D,由条件可知∠A=45°,∠B=30°,AC=10cm,可求得CD和AD,在Rt△BCD中可求得BD,再求△ABC面积即可.
解答: 解:如图,过点C作CD⊥AB于点D,
解:如图,过点C作CD⊥AB于点D,
∵sinA=
,cosB=
,
∴∠A=45°,∠B=30°,
∴AD=CD=
AC=5
cm,
∵tan∠B=
=
,
∴BD=
CD=5
,
∴AB=AD+BD=5
+5
,
∴S△ABC=
AB•CD=
×(5
+5
)×5
=25+25
(cm2).
 解:如图,过点C作CD⊥AB于点D,
解:如图,过点C作CD⊥AB于点D,∵sinA=
| ||
| 2 |
| ||
| 2 |
∴∠A=45°,∠B=30°,
∴AD=CD=
| ||
| 2 |
| 2 |
∵tan∠B=
| CD |
| BD |
| ||
| 3 |
∴BD=
| 3 |
| 6 |
∴AB=AD+BD=5
| 2 |
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 6 |
| 2 |
| 3 |
点评:本题主要考查特殊角的三角函数值,掌握30°、45°、60°特殊角的三角函数值是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
某小作坊第一天剥鸡头米10斤,计划第二、第三天共剥鸡头米28斤.设第二、第三天每天的平均增长率均为x,根据题意列出的方程是( )
| A、10(1+x)2=28 |
| B、10(1+x)+10(1+x)2=28 |
| C、10(1+x)=28 |
| D、10+10(1+x)+10(1+x)2=28 |
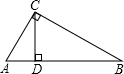 如图,在△ABC中,∠C=90°,CD⊥AB,D为垂足,求证:
如图,在△ABC中,∠C=90°,CD⊥AB,D为垂足,求证: 如图,将直角三角形顶点放在D(5,5)处,两直角边与坐标轴交点为E、F,则OE+OF的长是
如图,将直角三角形顶点放在D(5,5)处,两直角边与坐标轴交点为E、F,则OE+OF的长是