题目内容
 如图,将直角三角形顶点放在D(5,5)处,两直角边与坐标轴交点为E、F,则OE+OF的长是
如图,将直角三角形顶点放在D(5,5)处,两直角边与坐标轴交点为E、F,则OE+OF的长是考点:全等三角形的判定与性质,坐标与图形性质,角平分线的性质
专题:
分析:作DG⊥OG,DH⊥OF,易证∠GDE=∠FDH,即可证明△DEG≌△DFH,可得GE=FH,即可解题.
解答:解:作DG⊥OG,DH⊥OF,

∵∠GDE+∠EDH=90°,∠FDH+∠EDH=90°,
∴∠GDE=∠FDH,
∵在△DEG和△DFH中,
,
∴△DEG≌△DFH,(ASA)
∴GE=FH,
∴OE+OF=(OG-EG)+(OH+HF)=OG+OH=10.

∵∠GDE+∠EDH=90°,∠FDH+∠EDH=90°,
∴∠GDE=∠FDH,
∵在△DEG和△DFH中,
|
∴△DEG≌△DFH,(ASA)
∴GE=FH,
∴OE+OF=(OG-EG)+(OH+HF)=OG+OH=10.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△DEG≌△DFH是解题的关键.

练习册系列答案
相关题目
 已知:AC和BD相交于点E,AB∥DC,AB=DC,试说明:BE=DE.
已知:AC和BD相交于点E,AB∥DC,AB=DC,试说明:BE=DE. 如图,已知正方形ABCD与正方形CEFG,点G在边CD上,连接AF,取AF中点M,连接DM、GM.求证:
如图,已知正方形ABCD与正方形CEFG,点G在边CD上,连接AF,取AF中点M,连接DM、GM.求证: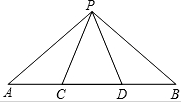 如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠APB=120°,△APC与△BPD相似吗?为什么?
如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠APB=120°,△APC与△BPD相似吗?为什么? 如图,直线AB、CD相交于点O,∠AOC=90°,∠1=∠2=∠3,∠4=∠5.
如图,直线AB、CD相交于点O,∠AOC=90°,∠1=∠2=∠3,∠4=∠5.