题目内容
已知Rt△ABC的斜边为AB,且它的外接圆的面积为4πcm2,则AB= .
考点:三角形的外接圆与外心
专题:计算题
分析:根据直角三角形的外心为直角三角形斜边的中点和圆的面积公式得到π•(
)2=4π,然后利用算术平方根的定义求AB的长.
| AB |
| 2 |
解答:解:∵Rt△ABC的斜边AB为它的外接圆的直径,
∴π•(
)2=4π,
∴AB=4(cm).
故答案为4cm.
∴π•(
| AB |
| 2 |
∴AB=4(cm).
故答案为4cm.
点评:本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.记住锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知点A(-2,1),点B(3,2),在x轴上求一点P,使AP+BP最小,下列作法正确的是( )
| A、点P与O(0.0)重合 |
| B、连接AB交y轴于P,点P即为所求. |
| C、过点A作x轴的垂线,垂足为P,点P即为所求 |
| D、作点B关于x轴的对称点C,连接AC,交x轴于P,点P即为所求 |
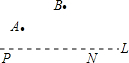 某市计划在一条公路L上修建一个火车站P和一个汽车站N,且使两站相距2km,在公路的一侧有景点A,B.如图所示旅客从P站坐车到两处游玩后,直接到N站坐汽车回到P站,则当P站修在公路何处时,能使旅客所走路程最短?
某市计划在一条公路L上修建一个火车站P和一个汽车站N,且使两站相距2km,在公路的一侧有景点A,B.如图所示旅客从P站坐车到两处游玩后,直接到N站坐汽车回到P站,则当P站修在公路何处时,能使旅客所走路程最短? 如图,已知正方形ABCD与正方形CEFG,点G在边CD上,连接AF,取AF中点M,连接DM、GM.求证:
如图,已知正方形ABCD与正方形CEFG,点G在边CD上,连接AF,取AF中点M,连接DM、GM.求证: 有一条长12m的木料做成如图的日字形窗框,请你计算出窗框的宽和高各取多少m时,这个窗框面积S最大.
有一条长12m的木料做成如图的日字形窗框,请你计算出窗框的宽和高各取多少m时,这个窗框面积S最大.