题目内容
7.如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.
(1)请你猜想BH和AC的关系,并说明理由
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).
分析 (1)BH=AC;证明△BDH≌△ADC即可;
(2)成立.证明思路同(1).
解答 证明:(1)BH=AC;如图1,
∵AD和BE是△ABC的高,
∴∠BDH=∠ADC=90°,∠DBH+∠C=∠CAD+∠C=90°,
∴∠DBH=∠DAC,
在△BDH和△ADC中,
$\left\{\begin{array}{l}{∠DBH=∠DAC}\\{BD=AD}\\{∠BDH=∠ADC}\end{array}\right.$,
∴△BDH≌△ADC(ASA),
∴BH=AC;
(2)成立,如图2,
∵AD和BE是△ABC的高,
∴∠BDH=∠ADC=90°,∠DBH+∠H=∠DBH+∠C=90°,
∴∠H=∠C,
在△BDH和△ADC中,
$\left\{\begin{array}{l}{∠H=∠C}\\{∠BDH=∠ADC}\\{AD=BD}\end{array}\right.$,
∴△BDH≌△ADC(AAS),
∴BH=AC.
点评 本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
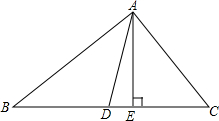 如图,AD是△ABC的中线,AE是△ABC的边BC上的高.
如图,AD是△ABC的中线,AE是△ABC的边BC上的高. 如图,AD∥BC,AE,BE分别平分∠DAB,∠ABC,CD过点E,求证:AB=AD+BC.
如图,AD∥BC,AE,BE分别平分∠DAB,∠ABC,CD过点E,求证:AB=AD+BC. 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图: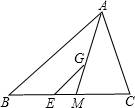 如图,点G为△ABC的重心,GE∥AB,求$\frac{BE}{CE}$的值.
如图,点G为△ABC的重心,GE∥AB,求$\frac{BE}{CE}$的值.