题目内容
17．两个多项式x+ax-1与x2+5x-6的乘积中不含x3项，试求a的值．分析 原式利用多项式乘以多项式法则计算，合并后根据乘积中不含有x3项，即可求出a的值．
解答 解：（x+ax-1）（x2+5x-6）=（a+1）x3+（5a+4）x2-（6a+11）x+6，
∵不含x3项，
∴a+1=0，
解得a=-1．
故a的值是-1．
点评 本题主要考查多项式与多项式的乘法，运算法则需要熟练掌握，不含某一项就让这一项的系数等于0是解题的关键．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
8．在一个不透明的布袋中装有4个除颜色外完全相同的小球，其中2个红球，1个白球，1个黄球．从中一次性摸出2个小球都是红球的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{8}$ |
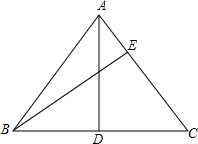如图，在△ABC中，AB=AC，∠ADB=90°，∠CBE=∠CAD，求证：△BEC∽△ADC．