题目内容
4.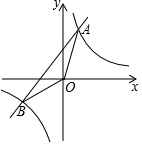 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2)、B两点.
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2)、B两点.(1)求A点的坐标及反比例函数的解析式;
(2)根据图象,当 y1<y2时,直接写出x的取值范围;
(3)点P是x轴上一点,且满足S△APB=3,直接写出点P的坐标.
分析 (1)根据直线解析式可得点A的坐标,根据点A的坐标可得反比例函数的解析式;
(2)先通过解方程组,得到两交点坐标,进而得到当 y1<y2时,x的取值范围;
(3)设直线与x轴的交点为C,点P的坐标为(a,0),根据S△APB=3,可得$\frac{1}{2}$×|-1-a|×(1+2)=3,求得a的值即可.
解答 解:(1)把y=2代入y=x+1得,2=x+1,
解得x=1,
∴A点的坐标为(1,2),
把A(1,2)代入y=$\frac{k}{x}$得,k=1×2=2,
∴反比例函数的解析式是y=$\frac{2}{x}$;
(2)联立两函数解析式,得$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{2}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-1}\end{array}\right.$,
∴点B的坐标为(-2,-1),
∴当 y1<y2时,x的取值范围是:x<-2或0<x<1;
(3)设直线与x轴的交点为C,点P的坐标为(a,0),
一次函数y1=x+1中,令y=0,则x=-1,
∴C(-1,0),
∴CP=|-1-a|,
由S△APB=3,可得$\frac{1}{2}$×|-1-a|×(1+2)=3,
解得a=1或-3,
∴P的坐标为(1,0)或(-3,0).
点评 本题主要考查了一次函数与反比例函数交点问题,解题时注意:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解即可.

练习册系列答案
相关题目
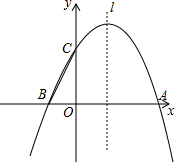 如图,二次函数y=ax2-2ax+3的图象与x轴交于点A,B,与y轴交于点C,∠CBO的正切值是3.
如图,二次函数y=ax2-2ax+3的图象与x轴交于点A,B,与y轴交于点C,∠CBO的正切值是3. 已知:如图所示,
已知:如图所示,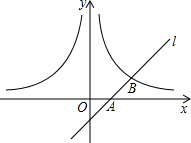 如图,直线l经过点A(1,0),且与双曲线y=$\frac{m}{x}$(x>0)交于点B(2,1),过点P(a,a-1)(a>1)作x轴的平行线分别交曲线y=$\frac{m}{x}$(x>0)和y=-$\frac{m}{x}$(x<0)于M,N两点.
如图,直线l经过点A(1,0),且与双曲线y=$\frac{m}{x}$(x>0)交于点B(2,1),过点P(a,a-1)(a>1)作x轴的平行线分别交曲线y=$\frac{m}{x}$(x>0)和y=-$\frac{m}{x}$(x<0)于M,N两点.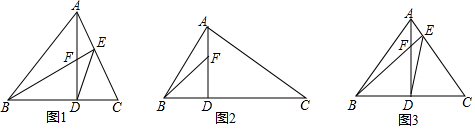
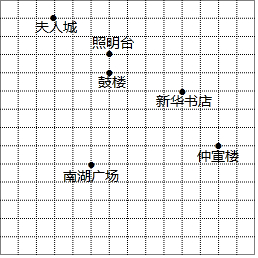 周末,小红、小丽、芳芳三位同学相约到仲宣楼游玩,出发前,她们每人带了一张用平面直角坐标系画的示意图,其中新华书店的坐标是(4,-1),南湖广场的坐标是(-1,-5).
周末,小红、小丽、芳芳三位同学相约到仲宣楼游玩,出发前,她们每人带了一张用平面直角坐标系画的示意图,其中新华书店的坐标是(4,-1),南湖广场的坐标是(-1,-5).