题目内容
12．
已知：如图所示，（1）画出△ABC关于y轴对称的△A′B′C′，并写出△A′B′C′三个顶点的坐标．
（2）在x轴上画出点P，使PA+PB最小（保留画图痕迹）
分析 （1）直接利用关于y轴对称点的性质得出各对应点位置进而得出答案；
（2）直接利用轴对称得出A点对应点，进而得出P点位置．
解答 
解：（1）如图所示：△A′B′C′，即为所求，
A′（-1，2），B′（-3，1），C′（-4，3）；
（2）如图所示：点P即为所求．
点评 此题主要考查了轴对称变换以及最短路线问题，正确得出对应点位置是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
3．
如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，点P第1次碰到矩形的边时，点P的坐标是（3，0），则当点P第2016次碰到矩形的边时，点P的坐标是（ ）
如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，点P第1次碰到矩形的边时，点P的坐标是（3，0），则当点P第2016次碰到矩形的边时，点P的坐标是（ ）| A． | （1，4） | B． | （0，3） | C． | （5，0） | D． | （8，3） |
20．下列各数中，不是无理数的是（ ）
| A． | $\sqrt{7}$ | B． | $\frac{11}{7}$ | C． | 4π | D． | $\root{3}{9}$ |
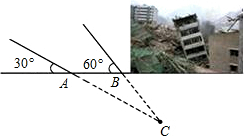某地震救援队探测出某建筑物废墟下方点C处有生命迹象，已知废墟一侧地面上两探测点A，B相距3米，探测线与地面的夹角分别是30°和60°（如图），则生命所在点C距离地面的深度是2.6米．（结果精确到0.1米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）
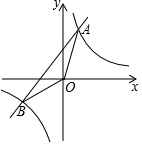如图，一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A（m，2）、B两点．
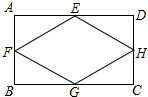如图，E、F、G、H分别为矩形ABCD四边的中点．
如图，△ABC中，∠C=90°，AD平分∠BAC，AB=7，CD=2，则△ABD的面积是7．