题目内容
14.已知下列一组数:-1,$\frac{3}{4}$,-$\frac{5}{9}$,$\frac{7}{16}$,$-\frac{9}{25}$,$\frac{11}{36}$…,则第9个数与第10个数之和为-$\frac{161}{8100}$.分析 由题意知,序数为奇数是为负数、序数为偶数时为正数,分子为序数的2倍与1的差,分母为序数的平方,据此得出第9、10个数,相加可得答案.
解答 解:∵第1个数-1=(-1)1×$\frac{2×1-1}{{1}^{2}}$,
第2个数$\frac{3}{4}$=(-1)2×$\frac{2×2-1}{{2}^{2}}$,
第3个数-$\frac{5}{9}$=(-1)3×$\frac{2×3-1}{{3}^{2}}$,
…
∴第9个数为(-1)9×$\frac{2×9-1}{{9}^{2}}$=-$\frac{17}{81}$,第10个数为(-1)10×$\frac{2×10-1}{1{0}^{2}}$=$\frac{19}{100}$,
则第9个数与第10个数之和为-$\frac{17}{81}$+$\frac{19}{100}$=-$\frac{161}{8100}$,
故答案为:-$\frac{161}{8100}$.
点评 本题主要考查数字的变化规律,根据数列得出序数为奇数是为负数、序数为偶数时为正数,分子为序数的2倍与1的差,分母为序数的平方是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
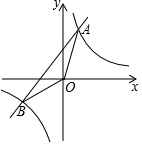 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2)、B两点.
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$的图象交于A(m,2)、B两点. 如图,△ABC中,∠C=90°,AD平分∠BAC,AB=7,CD=2,则△ABD的面积是7.
如图,△ABC中,∠C=90°,AD平分∠BAC,AB=7,CD=2,则△ABD的面积是7. 如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.