题目内容
14.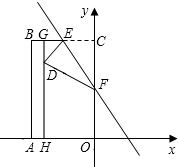 如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(-4,6),点E是BC的中点,点H在OA上,且AH=1,过点H且平行于y轴的HG与EB交于点G,现将矩形折叠,使顶点C落在HG上,并与HG上的点D重合,折痕为EF,点F为折痕与y轴的交点.CF=2$\sqrt{3}$.
如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(-4,6),点E是BC的中点,点H在OA上,且AH=1,过点H且平行于y轴的HG与EB交于点G,现将矩形折叠,使顶点C落在HG上,并与HG上的点D重合,折痕为EF,点F为折痕与y轴的交点.CF=2$\sqrt{3}$.(1)求点E和点D的坐标;
(2)求折痕EF所在直线的函数关系式;
(3)连接HC,求直线HC与EF的交点坐标.
(提示:$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$)
分析 (1)过点D作DM⊥y轴于点M,设CE=a,CM=b.根据边与边的关系以及翻折的特性可得出△EGD和△DMF各边的长度,根据勾股定理得出关于a、b的二元二次方程,解方程即可得出a、b值,根据a、b的值即可得出D、E的坐标;
(2)根据线段CF的长度找出F点的坐标,设折痕EF所在直线的函数关系式为y=kx+6-2$\sqrt{3}$,由点E的坐标利用待定系数法求出k值即可得出结论;
(3)结合H、C的坐标设出直线CH的函数关系式为y=k1x+6,由点H的坐标利用待定系数法求出直线CH的关系式,令y=2x+6=-$\sqrt{3}$x+6-2$\sqrt{3}$,求出x值,再将x代入到直线y=2x+6中求出y即可得出结论.
解答 解:(1)过点D作DM⊥y轴于点M,如图1所示.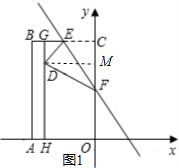
设CE=a,CM=b(0<a<3).
∵点B的坐标为(-4,6),
∴BC=AO=4,BA=CO=6,
∵AH=1,HG⊥x轴,
∴BG=AH=1,BA=GH=6,
∴GC=BC-BG=4-1=3.
∵CE=a,CM=b,
∴GD=b,GE=GC-CE=3-a,MF=CF-CM=2$\sqrt{3}$-b.
由翻折的特性可知:DE=CE,DF=CF.
由勾股定理可得$\left\{\begin{array}{l}{D{E}^{2}=G{D}^{2}+G{E}^{2}}\\{D{M}^{2}+M{F}^{2}=D{F}^{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{{a}^{2}={b}^{2}+(3-a)^{2}}\\{(2\sqrt{3})^{2}={3}^{2}+(2\sqrt{3}-b)^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{a=6}\\{b=3\sqrt{3}}\end{array}\right.$(舍去).
即CE=2,GD=$\sqrt{3}$,HD=GH-GD=6-$\sqrt{3}$.
故点E的坐标为(-2,6),点D的坐标为(-3,6-$\sqrt{3}$).
(2)∵OF=CO-CF=6-2$\sqrt{3}$,
∴点F的坐标为(0,6-2$\sqrt{3}$).
设折痕EF所在直线的函数关系式为y=kx+6-2$\sqrt{3}$.
∵点E(-2,6)在直线EF上,
∴有6=-2k+6-2$\sqrt{3}$,解得:k=-$\sqrt{3}$,
∴折痕EF所在直线的函数关系式为y=-$\sqrt{3}$x+6-2$\sqrt{3}$.
(3)根据题意画出图形,如图2.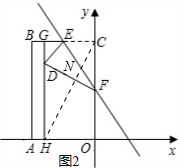
点C的坐标为(0,6),点H的坐标为(-3,0).
设直线CH的函数关系式为y=k1x+6,
将点H(-3,0)的坐标代入y=k1x+6中,
得0=-3k1+6,解得:k1=2.
∴直线CH的函数关系式为y=2x+6.
令y=2x+6=-$\sqrt{3}$x+6-2$\sqrt{3}$,解得:x=6-4$\sqrt{3}$,
将x=6-4$\sqrt{3}$代入y=2x+6中,得:y=18-8$\sqrt{3}$.
∴直线HC与EF的交点坐标为(6-4$\sqrt{3}$,18-8$\sqrt{3}$).
点评 本题考查了解二元二次方程组、待定系数法求函数解析式、勾股定理以及两直线的交点,解题的关键:(1)结合勾股定理得出关于a、b的二元二次方程组;(2)由待定系数法求出函数解析式;(3)由待定系数法求出函数解析式,再求出两直线的交点.本题属于中档题,难度不大,解决该题型题目时,由待定系数法求出函数解析式是关键.

| A. | -1 | B. | 1 | C. | 3 | D. | 3或-1 |
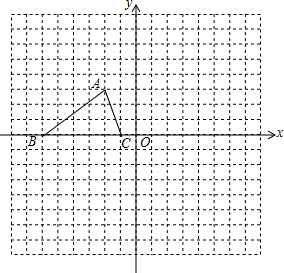 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).将△ABC绕坐标原点O逆时针旋转90°,得到△A′B′C′,画出△A′B′C′.并计算点A旋转经过的路径长度.
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).将△ABC绕坐标原点O逆时针旋转90°,得到△A′B′C′,画出△A′B′C′.并计算点A旋转经过的路径长度.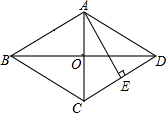 如图,已知菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分边CD,垂足为E,求∠BCD的度数.
如图,已知菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分边CD,垂足为E,求∠BCD的度数. 如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形.
如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形.