题目内容
10.比较大小:$\sqrt{10}$> π;$\sqrt{\frac{1}{10}}$>$\frac{1}{10}$;$\sqrt{2}$<2.分析 求出π2和$\sqrt{10}$的平方的值比较,把$\sqrt{\frac{1}{10}}$,$\frac{1}{10}$与$\sqrt{2}$,2两个数平方法,由于两数均为正数,所以该数的平方越大数越大.
解答 解:∵π2<10,
∴π<$\sqrt{10}$.
∵$(\sqrt{\frac{1}{10}})^{2}=\frac{1}{10}$=$\frac{10}{100}$,$(\frac{1}{10})^{2}=\frac{1}{100}$,
∴$\frac{1}{10}>\frac{1}{100}$,
∴$\sqrt{\frac{1}{10}}>\frac{1}{100}$,
∵$(\sqrt{2})^{2}$=2,22=4,
∴2<4,
∴$\sqrt{2}<2$,
故答案为:>;>;<.
点评 本题考查了实数的大小比较的应用,能正确比较两无理数的大小是解此题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
20. 实数a,b,c在数轴上的对应点的位置如图所示,下列各项成立的是( )
实数a,b,c在数轴上的对应点的位置如图所示,下列各项成立的是( )
 实数a,b,c在数轴上的对应点的位置如图所示,下列各项成立的是( )
实数a,b,c在数轴上的对应点的位置如图所示,下列各项成立的是( )| A. | c-b>a | B. | b+a>c | C. | ac>b | D. | ab>c |
5.下列从左到右的变形属于因式分解的是( )
| A. | x2-9+6x=(x+3)(x-3)+6x | B. | (x+5)(x-2)=x2+3x-10 | ||
| C. | x2-8x+16=(x-4)2 | D. | -6a2b=-3a﹒2ab |

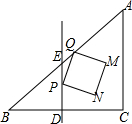 如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).
如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).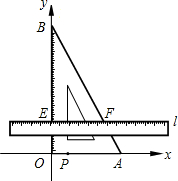 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.