题目内容
9.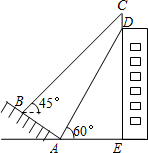 如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,进而可求出EF即BG的长;在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长;根据CD=CG+GE-DE即可求出宣传牌的高度.
解答 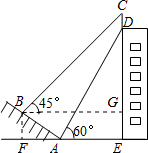 解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,i=tan∠BAF=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BAF=30°,
∴BF=$\frac{1}{2}$AB=10,AF=10$\sqrt{3}$.
∴BG=AF+AE=10$\sqrt{3}$+30.
Rt△BGC中,∠CBG=45°,
∴CG=BG=10$\sqrt{3}$+30.
Rt△ADE中,∠DAE=60°,AE=30,
∴DE=$\sqrt{3}$AE=30$\sqrt{3}$.
∴CD=CG+GE-DE=10$\sqrt{3}$+30+10-30$\sqrt{3}$=40-20$\sqrt{3}$≈5.4m.
答:宣传牌CD高约5.4米.
点评 此题综合考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
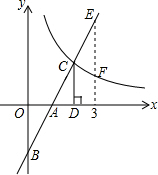 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论: 如图,已知二次函数y=ax2+bx+2的图象顶点为(-1,0),下列结论:①a<0;②abc>0;③b2+4ac=0;④4a-2b+c<0.其中正确结论的是②(只填写序号).
如图,已知二次函数y=ax2+bx+2的图象顶点为(-1,0),下列结论:①a<0;②abc>0;③b2+4ac=0;④4a-2b+c<0.其中正确结论的是②(只填写序号).



 如图,已知AB∥CD,试找出∠B、∠BEF,∠EFD以及∠D之间数量关系,并说明理由.
如图,已知AB∥CD,试找出∠B、∠BEF,∠EFD以及∠D之间数量关系,并说明理由. 如图,己知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
如图,己知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么? B.
B.  C. -5 D. 5
C. -5 D. 5