题目内容
7.按要求用直尺作图(可以添加辅助线辅助作图):(1)△ABC的三个顶点都在如图(1)所示的正方形网格的格点上,请在正方形网格中画出△ABC关于点O逆时针旋转180°的△A′B′C′.
(2)如图(2)平行四边形草地内有一圆形空坝(有圆心标记,见图).请画一直线AB,能同时做到把平行四边形和圆的面积二等分.
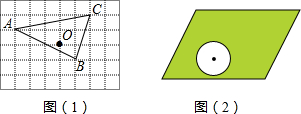
分析 (1)利用网格特点和中心对称的性质分别画出点A、B、C的对应点A′、B′、C′,则可得到△A′B′C′;
(2)根据中心对称图形的性质,先画出平行四边形的对角线的交点,然后连结圆心和对角线的交点即可.
解答 解:(1)如图1,△A′B′C′为所作;
(2)如图2,AB为所作;
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
17.已知1是关于x的一元二次方程x2+(m-1)x+1=0的一个根,则m的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
2.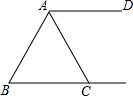 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )| A. | 50° | B. | 25° | C. | 60° | D. | 65° |
12.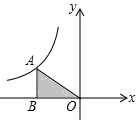 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )
 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )| A. | $y=-\frac{2}{x}$ | B. | $y=\frac{2}{x}$ | C. | $y=-\frac{4}{x}$ | D. | $y=\frac{4}{x}$ |
16.下列命题中,是真命题的( )
| A. | 同一平面内,两条直线一定互相平行 | |
| B. | 若a∥b,b∥c,则a∥c | |
| C. | 若a 2=b 2,则a=b | |
| D. | 从直线外一点到这条直线的垂线段,叫做点到直线的距离 |
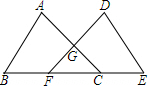 如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:
如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证: 某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.
某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.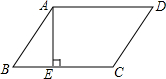 如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长.
如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长.