题目内容
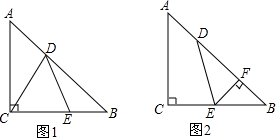
10.△ABC中,AC=BC,∠ACB=90°,点D在AB上,E在BC上,且AD=BE,BD=AC.(1)如图1,连接DE,CD.
①找出图中全等三角形,并证明;
②求∠ACD的度数;
(2)如图2,过E作EF⊥AB于F,若BF=4,求CE的长.
分析 (1)①根据等腰三角形的性质和SAS可证△BDE≌△ACD,②再根据等腰直角三角形的性质即可得到∠ACD的度数;
(2)连CD,由(1)知CD=DE,根据等腰三角形的性质和角的和差关系可得∠CDE=45°,过D作DM⊥CE于M,根据角平分线的性质以及等量关系即可得到CE的长.
解答 (1)①△ADC≌△BED,
证明:∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠B=45°,
在△ADC和△BED中
$\left\{\begin{array}{l}{AD=BE}\\{∠A=∠B}\\{AC=BD}\end{array}\right.$
∴△ADC≌△BED(SAS);
②解:∵△ADC≌△BED,
∴∠ACD=∠BDE,
∵∠B=45°,BC=BD,
∴∠BCD=67.5°,
∵∠ACB=90°,
∴∠ACD=22.5°;
(2)解:连CD,由(1)知CD=DE,
∴∠DCE=∠DEC=67.5°,
∴∠CDE=45°,
过D作DM⊥CE于M,
∴CM=ME,∠CDM=∠EDM=∠BDE=22.5°,
∵EM⊥DM,EF⊥DB,
∴EF=EM,
易证EF=BF,
∴CE=2BF=8.
点评 本题考查了等腰直角三角形的性质的运用,等腰三角形的性质的运用,全等三角形的判定及性质的运用,解答时添加合适的辅助线是难点.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
2.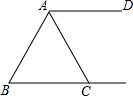 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )| A. | 50° | B. | 25° | C. | 60° | D. | 65° |
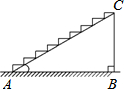 如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.
如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.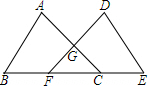 如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:
如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证: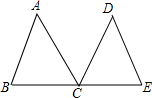 如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC.
如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC. 某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.
某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.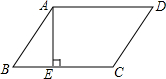 如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长.
如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长.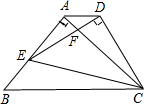 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤.