题目内容
18．
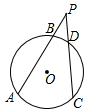如图，当⊙O中的弦AB，CD的延长线相交于点P时，探索∠APC的度数与$\widehat{AC}$，$\widehat{BD}$的度数之间的数量关系．
分析 根据圆周角得到了得到∠ABC=$\frac{1}{2}$×$\widehat{AC}$的度数，∠BCD=$\frac{1}{2}$×$\widehat{BD}$的度数，根据三角形的外角的性质计算即可．
解答 解：
∠APC=$\frac{1}{2}$×（$\widehat{AC}$+$\widehat{BD}$）的度数．
连接BC，
由圆周角定理得，∠ABC=$\frac{1}{2}$×$\widehat{AC}$的度数，∠BCD=$\frac{1}{2}$×$\widehat{BD}$的度数，
∴∠APC=∠ABC-∠BCD=$\frac{1}{2}$×（$\widehat{AC}$+$\widehat{BD}$）的度数．
点评 本题考查的是圆心角、弧、弦的关系定理、圆周角定理的应用，在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
一课一练课时达标系列答案
相关题目
如图，⊙O的直径CD=8，AB是⊙O的弦，AB⊥CD于M，且CM=2，则AB的长为4$\sqrt{3}$．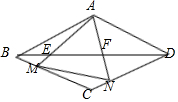
已知：菱形ABCD中，∠BAD=120°，M、N分别是BC、CD边上的点，且△AMN是等边三角形．
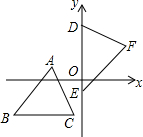如图，坐标平面上，△ABC≌△DEF，且AB=BC=9．若A点的坐标为（-3，1），B、C两点在直线y=-5上，D、E两点在y轴上，则点F到y轴的距离为（ ）
如图，已知OA=OB．