题目内容
12.已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.(1)如图①,求证:AC=CD;
(2)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.
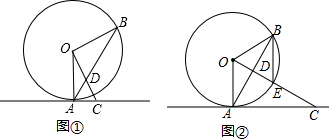
分析 (1)如图①,先利用切线的性质得∠OAB+∠CAB=90°,再利用OC⊥OB得到∠B+∠ODB=90°,然后根据对顶角相等和等腰三角形的性质得到∠ODB=∠ADC,∠OAB=∠B,则可判断∠ADC=∠CAB,于是利用等腰三角形的判定定理即可得到结论;
(2)如图②,先判断△OBE为等腰直角三角形得到∠OEB=45°,再根据平行线的性质得到∠AOC=∠OEB=45°,则可判断△OAC为等腰直角三角形,所以AC=OA=1,OC=$\sqrt{2}$OA=$\sqrt{2}$,然后利用(1)中的结论得到CD=CA=1,于是计算OC-CD即可.
解答 (1)证明:如图①,
∵直线AC与⊙O相切,
∴OA⊥AC,
∴∠OAC=90°,即∠OAB+∠CAB=90°,
∵OC⊥OB,
∴∠BOC=90°,
∴∠B+∠ODB=90°,
而∠ODB=∠ADC,
∴∠ADC+∠B=90°,
∴OA=OB,
∴∠OAB=∠B,
∴∠ADC=∠CAB,
∴AC=CD;
(2)解:如图②,
∴∠BOC=90°,OB=OE,
∴△OBE为等腰直角三角形,
∴∠OEB=45°,
∵BE∥OA,
∴∠AOC=∠OEB=45°,
∴△OAC为等腰直角三角形,
∴AC=OA=1,OC=$\sqrt{2}$OA=$\sqrt{2}$,
而CD=CA=1,
∴OD=OC-CD=$\sqrt{2}$-1.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等腰三角形的性质和等腰直角三角形的判定与性质.

练习册系列答案
相关题目
2.在某次体育测试中,某小组8位同学的成绩分别是66,67,78,78,79,79,79,80,则这8人体育成绩的众数是( )
| A. | 77 | B. | 78 | C. | 78.5 | D. | 79 |
20. 如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )
如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )
 如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )
如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )| A. | 110° | B. | 100° | C. | 90° | D. | 80° |
17.2008年6月1日起,全国商品零售场所开始实行:塑料购物袋有偿使用制度”,截止2016年5月底全国大约节约塑料购物袋66.8亿个,这个数用科学记数法表示为( )
| A. | 0.668×109 | B. | 6.68×10-9 | C. | 6.68×109 | D. | 66.8×108 |
4. 如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
 如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过(-3,0),对称轴直线为x=-1,给出四个结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过(-3,0),对称轴直线为x=-1,给出四个结论: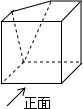 如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )
如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )

 如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.
如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.