题目内容
8.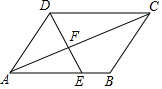 如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
分析 由$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$推出AF:FC=2:3,由四边形ABCD是平行四边形,推出CD∥AB,推出$\frac{AE}{CD}$=$\frac{AF}{CF}$=$\frac{2}{3}$,由此即可解决问题.
解答 解:∵$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,
∴AF:FC=2:3,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴△AEF∽△CDF,
∴$\frac{AE}{CD}$=$\frac{AF}{CF}$=$\frac{2}{3}$,
∵CD=6,
∴AE=4,
故答案为4.
点评 本题考查相似三角形的性质、平行四边形的性质等知识,解题的关键是灵活应用所学知识解决问题,求出AF:CF的值是关键,属于中考常考题型.

练习册系列答案
相关题目
20.若正数a是一元二次方程x2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,则a的值是( )
| A. | $\frac{5}{2}$ | B. | $-\frac{5}{2}$ | C. | -5 | D. | 5 |
17.下列函数中,是反比例函数的是( )
| A. | y=$\frac{k}{x}$ | B. | 3x+2y=0 | C. | xy-$\sqrt{2}$=0 | D. | y=$\frac{2}{x+1}$ |
18.下列交通标志图形好是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
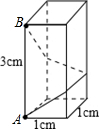 如图,长方体的底面是边长为1cm 的正方形,高为3cm.
如图,长方体的底面是边长为1cm 的正方形,高为3cm.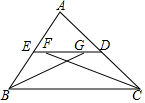 如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8.
如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8. 如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么亮亮画图的依据是两角和它们的夹边分别相等的两个三角形全等.
如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么亮亮画图的依据是两角和它们的夹边分别相等的两个三角形全等.