题目内容
3.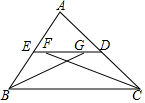 如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8.
如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC=8.
分析 只要证明EG=EB,DF=DC即可解决问题.
解答 解: ∵ED∥BC,
∵ED∥BC,
∴∠EGB=∠GBC,∠DFC=∠FCB,
∵∠GBC=∠GBE,∠FCB=∠FCD,
∴∠EGB=∠EBG,∠DCF=∠DFC,
∴BE=EG,CD=DF,
∵FG=2,ED=6,
∴EB+CD=EG+DF=EF+FG+FG+DG=ED+FG=8,
故答案为8.
点评 本题考查等腰三角形的判定和性质、角平分线的定义,平行线的性质等知识,解题的关键是等腰三角形的证明,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.立方是它本身的数是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 1,-1,0 |
8.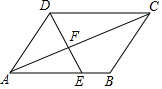 如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
 如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
13.已知关于x的一元二次方程x2+ax+b=0有一个非零根-b,则a-b的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
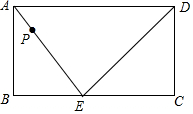 如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.
如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.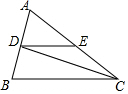 如图,已知在△ABC中,CD平分∠ACB,且CD⊥AB于D,DE∥BC交AC于点E,AC=3cm,AB=2cm,则△ADE的周长为4cm.
如图,已知在△ABC中,CD平分∠ACB,且CD⊥AB于D,DE∥BC交AC于点E,AC=3cm,AB=2cm,则△ADE的周长为4cm. 如图,在平面直角坐标系中,点C在y轴上,点A(a,0)、点B(a-4,0),位于原点两侧,且∠ABC=60°,AE⊥BC,交y轴于点F,交BC于点E,点D在点B的左侧,且∠CDO=45°,AB=2BD
如图,在平面直角坐标系中,点C在y轴上,点A(a,0)、点B(a-4,0),位于原点两侧,且∠ABC=60°,AE⊥BC,交y轴于点F,交BC于点E,点D在点B的左侧,且∠CDO=45°,AB=2BD 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是在角的内部,到角两边距离相等的点在角的平分线上.
小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是在角的内部,到角两边距离相等的点在角的平分线上.