题目内容
20.若正数a是一元二次方程x2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,则a的值是( )| A. | $\frac{5}{2}$ | B. | $-\frac{5}{2}$ | C. | -5 | D. | 5 |
分析 把x=a代入方程x2-5x+m=0,得a2-5a+m=0①,把x=-a代入方程方程x2+5x-m=0,得a2-5a-m=0②,再将①+②,即可求出a的值.
解答 解:∵a是一元二次方程x2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,
∴a2-5a+m=0①,a2-5a-m=0②,
①+②,得2(a2-5a)=0,
∵a>0,
∴a=5.
故选D.
点评 本题主要考查的是一元二次方程的根即方程的解的定义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
8.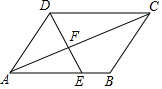 如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
 如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
如图,在平行四边形ABCD中,点E在边AB上,联结DE,交对角线AC于点F,如果$\frac{{S}_{△ADF}}{{S}_{△DFC}}$=$\frac{2}{3}$,CD=6,那么AE=4.
5.若单项式-3a5b与amb是同类项,则常数m的值为( )
| A. | 5 | B. | 2 | C. | 1 | D. | -3 |
9.2015年诺贝尔奖得主中国女药学家屠呦呦在演讲中提到:“据统计,2013年全球疟疾患者约为1亿9千8百万,疟疾导致的死亡人数约为58万,其中78%是5岁以下的儿童,90%的疟疾死亡病例发生在重灾区非洲.”其中58万用科学记数法表示是( )
| A. | 0.58×106 | B. | 5.8×106 | C. | 58×104 | D. | 5.8×105 |
10. 如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′处,若∠l=112°,则∠BFC′的度数是( )
如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′处,若∠l=112°,则∠BFC′的度数是( )
 如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′处,若∠l=112°,则∠BFC′的度数是( )
如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′处,若∠l=112°,则∠BFC′的度数是( )| A. | 44° | B. | 62° | C. | 68° | D. | 124° |

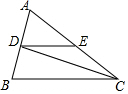 如图,已知在△ABC中,CD平分∠ACB,且CD⊥AB于D,DE∥BC交AC于点E,AC=3cm,AB=2cm,则△ADE的周长为4cm.
如图,已知在△ABC中,CD平分∠ACB,且CD⊥AB于D,DE∥BC交AC于点E,AC=3cm,AB=2cm,则△ADE的周长为4cm. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是在角的内部,到角两边距离相等的点在角的平分线上.
小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是在角的内部,到角两边距离相等的点在角的平分线上.