题目内容
 有一工程勘测队为测量某个山坡上无法到达的A,B两处之间的距离,测得如下一些数据,如图,在山腰P处测得对面山脚A处的俯角(即∠FPA)为60°,测得对面山坡上B处的俯角(即∠FPB)为35°,已知∠BAC=30°,点P,E,A,B,C在同一平面上,点E,A,C在同一直线上,且PE⊥EC,AE=100米.
有一工程勘测队为测量某个山坡上无法到达的A,B两处之间的距离,测得如下一些数据,如图,在山腰P处测得对面山脚A处的俯角(即∠FPA)为60°,测得对面山坡上B处的俯角(即∠FPB)为35°,已知∠BAC=30°,点P,E,A,B,C在同一平面上,点E,A,C在同一直线上,且PE⊥EC,AE=100米.(1)经计算,得∠PAB的度数为
(2)求出A,B两点之间的距离.(结果精确到0.1米)
(参考数据:sin25°≈0.4226,cos25°≈0.9063,tan25°≈0.4663)
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:(1)求出∠PAE=60°,用180°-∠BAC-∠PAE即可;
(2)求出AP的长,求出∠APB的度数,从而得到AB的长.
(2)求出AP的长,求出∠APB的度数,从而得到AB的长.
解答:解:(1)∵∠FPA=60°,
∴∠PAE=60°,
又∵∠BAC=30°,
∴∠PAB=180°-60°-30°=90°;
(2)∵∠FPA=60°,
∴∠EPA=90°-60°=30°,
又∵∠EPA=30°,
∴AP=100×2=200米,
∵∠FPB=35°,∠FPA=60°,
∴∠APB=60°-35°=25°,
∴AB=AP•tan25°=200×0.4663=93.26米.
故答案为90°.
∴∠PAE=60°,
又∵∠BAC=30°,
∴∠PAB=180°-60°-30°=90°;
(2)∵∠FPA=60°,
∴∠EPA=90°-60°=30°,
又∵∠EPA=30°,
∴AP=100×2=200米,
∵∠FPB=35°,∠FPA=60°,
∴∠APB=60°-35°=25°,
∴AB=AP•tan25°=200×0.4663=93.26米.
故答案为90°.
点评:本题考查解直角三角形的应用--仰角俯角问题,要求学生能借助仰角、俯角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A、四棱锥 | B、四棱柱 |
| C、三棱锥 | D、三棱柱 |
下列长度的各种线段,可以组成三角形的是( )
| A、1,2,3 |
| B、1,5,5 |
| C、3,3,6 |
| D、1,5,6 |
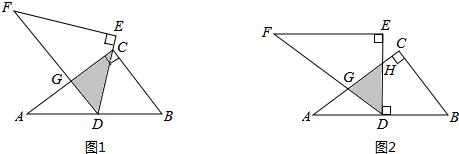
 如图,一只蚂蚁在长方体木块的一个顶点A处,食物在这个长方体上和蚂蚁相对的顶点B处,蚂蚁急于吃到食物,所以沿着长方体的表面上向上爬,请你计算出它从A处爬到B处的最短路线长为多少?
如图,一只蚂蚁在长方体木块的一个顶点A处,食物在这个长方体上和蚂蚁相对的顶点B处,蚂蚁急于吃到食物,所以沿着长方体的表面上向上爬,请你计算出它从A处爬到B处的最短路线长为多少?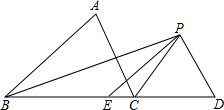 已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长.
已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长. 如图所示,OA,OB,OC都是⊙O的半径,∠ACB=45°,∠BOC=30°,求∠BAC与∠AOB的度数.
如图所示,OA,OB,OC都是⊙O的半径,∠ACB=45°,∠BOC=30°,求∠BAC与∠AOB的度数. 如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若DP=6,则PE的长为( )
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若DP=6,则PE的长为( )