题目内容
17.已知数轴上A,B两点对应数分别为a和b,且a、b满足等式(a+9)2+|7-b|=0,P为数轴上一动点,对应数为x.(1)求线段AB的长.
(2)数轴上是否存在P点,使PA=3PB?若存在,求出x的值;若不存在,请说明理由.
(3)在(2)的条件下,若点M、点N分别是线段AB,PB的中点,试求线段MN的长.
分析 (1)根据非负数的和等于零,可得每个非负数同时为零,根据数轴上两点间的距离是大数减小数,可得答案;
(2)根据线段的和差,可得关于PB的方程,根据解方程,可得PB的长,根据数轴上的两点间的距离,可得x;
(3)根据线段中点的性质,可得MB,NB,根据线段的和差,可得答案.
解答 解:(1)由(a+9)2+|7-b|=0,得
a+9=0,7-b=0.
解得a=-9,b=7.
线段AB的长为b-a=7-(-9)=16;
(2)当P在AB上时,PA+PB=AB,即3PB+PB=AB,
即PB=4,
7-x=4,解得x=3;
当P在线段AB的延长线上时,PA-PB=AB,
3PB-PB=AB,
PB=8,
x=7+8=15;
(3)当P在AB上时,如图1; ,
,
点M、点N分别是线段AB,PB的中点,得
MB=$\frac{1}{2}$AB=8,BN=$\frac{1}{2}$PB=2.
由线段的和差,得
MN=MB-NB=8-2=6;
当P在AB的延长线上时,如图2; ,
,
点M、点N分别是线段AB,PB的中点,得
MB=$\frac{1}{2}$AB=8,BN=$\frac{1}{2}$PB=4.
由线段的和差,得
MN=MB-NB=8+4=12.
综上所述:MN的长为6或12.
点评 本题考查了两点间的距离,利用线段的和差得PB的长是解题关键,又利用了线段中点的性质,要分类讨论,以防遗漏.

练习册系列答案
相关题目
7.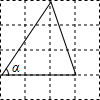 如图,在4×4的正方形网格中,tanα的值等于( )
如图,在4×4的正方形网格中,tanα的值等于( )
 如图,在4×4的正方形网格中,tanα的值等于( )
如图,在4×4的正方形网格中,tanα的值等于( )| A. | $\frac{{2\sqrt{13}}}{13}$ | B. | $\frac{{3\sqrt{13}}}{13}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
8.下列从左到右的变形,是因式分解的是( )
| A. | (x-1)(x=2)=(x+2)(x-1) | B. | m2-1=(m+1)(m-1) | ||
| C. | x2+1=x(x+$\frac{1}{x}$) | D. | a(a-b)(b+1)=(a2-ab)(b+1) |
5.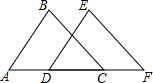 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )| A. | BC=EF | B. | ∠A=∠EDF | C. | AB∥DE | D. | ∠BCA=∠F |
12.下列运算正确的是( )
| A. | (x3)2=x5 | B. | x2+x3=x5 | C. | 3-2=$\frac{1}{9}$ | D. | 6x3÷(-3x2)=2x |
2.如果点(a,1-a)在第四象限,那么a的取值范围是( )
| A. | 0<a<1 | B. | -1<a<0 | C. | a<0 | D. | a>1 |
9.二次函数y=-3(x-4)2+5的开口方向、对称轴、顶点坐标分别是( )
| A. | 向下、直线x=4、(4,5) | B. | 向下、直线x=-4、(-4,5) | ||
| C. | 向上、直线x=4、(4,5) | D. | 向上、直线x=-4、(-4,-5) |
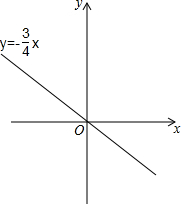 一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C.
一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C. 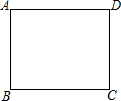 如图,某广场为矩形ABCD,现准备在广场的内部修建照明灯,要求照明灯0到广场的两个人口A,D的距离相等,且到AB,BC两边的距离相等.
如图,某广场为矩形ABCD,现准备在广场的内部修建照明灯,要求照明灯0到广场的两个人口A,D的距离相等,且到AB,BC两边的距离相等.