题目内容
20.化简求值:($\frac{a}{a+3}+\frac{a+1}{{a}^{2}-9}$)÷$\frac{a-1}{a+3}$+$\frac{1}{a-3}$,中a=3+$\sqrt{3}$.分析 先算括号内的加法,同时把除法变成乘法,再算乘法,最后算加法,代入求出答案即可.
解答 解:($\frac{a}{a+3}+\frac{a+1}{{a}^{2}-9}$)÷$\frac{a-1}{a+3}$+$\frac{1}{a-3}$
=[$\frac{a(a-3)}{(a+3)(a-3)}$+$\frac{a+1}{(a+3)(a-3)}$]•$\frac{a+3}{a-1}$+$\frac{1}{a-3}$
=$\frac{(a-1)^{2}}{(a+3)(a-3)}$•$\frac{a+3}{a-1}$+$\frac{1}{a-3}$
=$\frac{a-1}{a-3}$+$\frac{1}{a-3}$
=$\frac{a-1+1}{a-3}$
=$\frac{a}{a-3}$,
当a=3+$\sqrt{3}$时,原式=$\frac{3+\sqrt{3}}{3+\sqrt{3}-3}$=1+$\sqrt{3}$.
点评 本题考查了分式的混合运算和求值,能正确根据分式的运用法则进行化简是解此题的关键,注意运算顺序.

练习册系列答案
相关题目
10.-4的绝对值等于( )
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -4 | D. | 4 |
11.某网站数据显示,2015年第一季度我国彩电销量为1233万台,将1233万用科学记数法可表示为( )
| A. | 12.33×105 | B. | 1.233×103 | C. | 0.1233×108 | D. | 1.233×107 |
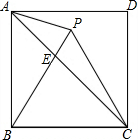 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论: