题目内容
9. 如图,AD、AE分别是△ABC的中线和角平分线,AC=2,AB=5,过点C作CF⊥AE于点F,连接DF,有下列结论:
如图,AD、AE分别是△ABC的中线和角平分线,AC=2,AB=5,过点C作CF⊥AE于点F,连接DF,有下列结论:①将△ACF沿着直线AE折叠,点C怡好落在AB上;
②3<2AD<7;
③若∠B=30°,∠FCE=15°,则∠ACB=55°;
④若△ABC的面积为S,则△DFC的面积为0.15S.
其中正确的是①②④.(把所有正确结论的序号都选上)
分析 如图延长CF交AB于M,延长AD到N使得DN=AD,连接BN、CN;①正确,由CF=CM即可解决.②正确,在△ABN中利用三边关系即可解决.③错误,∠ACB=60°,④正确,先证明S△BCM=$\frac{3}{5}$S△ABC=$\frac{3}{5}$s,由△DFC∽△BMC,得S△DFC=$\frac{1}{4}$S△BCM即可证明.
解答 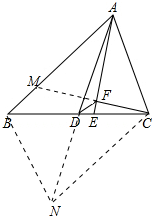 解;如图延长CF交AB于M,延长AD到N使得DN=AD,连接BN、CN,
解;如图延长CF交AB于M,延长AD到N使得DN=AD,连接BN、CN,
∵∠FAM=∠FAC,∠AFM=∠AFC=90°,
∴∠FAM+∠AMF=90°,∠FAC+∠ACF=90°,
∴∠AMC=∠ACM,
∴AM=AC,∵AF⊥MC,
∴MF=CF,
∴将△ACF沿着直线AE折叠,点C怡好落在AB上,故①正确.
∵BD=CD,AD=DN,
∴四边形ABNC是平行四边形,
∴BN=AC=2,∵AB=5,
在△ABN中,有5-2<AN<5+2,
∴3<2AD<7,故②正确,
∵∠B=30°,∠FCE=15°,
∴∠AMC=∠ACM=45°,
∴∠ACB=∠ACM+∠FCE=60°,故③错误.
∵AM=AC=2,AB=5,
∴BM:AB=3:5,
∴S△BCM=$\frac{3}{5}$S△ABC=$\frac{3}{5}$s,
∵BD=CD,MF=FC,
∴DF∥BM,
∴△DFC∽△BMC,
∴S△DFC=$\frac{1}{4}$S△BCM=$\frac{3}{20}s$=0.15s,故④正确,
故答案为①②④.
点评 本题考查翻折变换、全等三角形的判定和性质、等腰三角形的判定和性质,解题的关键是添加辅助线构造特殊三角形或特殊四边形,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.我市一水果销售公司,需将一批鲜桃运往某地,有汽车、火军两种运输工具可供选择,两种运输工具的主要参考数据如下:
假设这批水果在运输过程中(含装卸时间)的损耗为160元/时.
(1)当运输路程为400千米时,你认为采用哪种运输工具比较好?
(2)当运输路程为多少千米时,两种运输工具所需总费用相同.
| 运输工具 | 途中平均费用(单位:元/千米) | 途中平均速度(单位:千米/时) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
| 汽车 | 10 | 80 | 2 | 1000 |
| 火车 | 8 | 100 | 4 | 2000 |
(1)当运输路程为400千米时,你认为采用哪种运输工具比较好?
(2)当运输路程为多少千米时,两种运输工具所需总费用相同.
14.有下列几种说法:
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交所成的四个角中有一组相邻补角相等;
④两条直线相交对顶角互补.
其中,能两条直线互相垂直的是( )
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交所成的四个角中有一组相邻补角相等;
④两条直线相交对顶角互补.
其中,能两条直线互相垂直的是( )
| A. | ①③ | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
19.下列计算正确的是( )
| A. | a3+a3=a6 | B. | (2a)3=2a3 | C. | (a3)2=a5 | D. | a•a5=a6 |
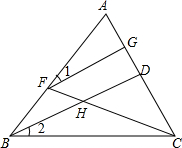 如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.
如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.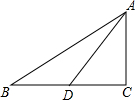 如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.