题目内容
6. 如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积$\frac{7\sqrt{3}}{2}$.
如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积$\frac{7\sqrt{3}}{2}$.
分析 根据平行四边形的性质和折叠的性质得出∠B=∠G,∠BCE=∠GCF,BC=GC,然后根据AAS证明△BCE≌△GCF,得出CE=CF,过E点作EP⊥BC于P,设BP=m,则BE=2m,通过解直角三角形求得EP=$\sqrt{3}$m,然后根据折叠的性质和勾股定理求得EC,进而根据三角形的面积即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠A=∠BCD,
由折叠可知,AD=CG,∠D=∠G,∠A=∠ECG,
∴BC=GC,∠B=∠G,∠BCD=∠ECG,
∴∠BCE=∠GCF,
在△BCE和△GCF中,$\left\{\begin{array}{l}{∠B=∠G}&{\;}\\{∠BCE=∠GCF}&{\;}\\{BC=GC}&{\;}\end{array}\right.$,
∴△BCE≌△GCF(ASA),
∴CE=CF,
过E点作EP⊥BC于P,如图所示:
∵∠B=60°,∠EPB=90°,
∴∠BEP=30°,
∴BE=2BP,
设BP=m,则BE=2m,
∴EP=BE•sin60°=2m×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$m,
由折叠可知,AE=CE,
∵AB=6,
∴AE=CE=6-2m,
∵BC=4,
∴PC=4-m,
在RT△ECP中,由勾股定理得(4-m)2+($\sqrt{3}$m)2=(6-2m)2,
解得:m=$\frac{5}{4}$,
∴CE=6-2m=6-2×$\frac{5}{4}$=$\frac{7}{2}$,
∵△BCE≌△GCF,
∴CF=CE=$\frac{7}{2}$,
∴S△CEF=$\frac{1}{2}$×$\frac{7}{2}$×2$\sqrt{3}$=$\frac{7\sqrt{3}}{2}$;
故答案为:$\frac{7\sqrt{3}}{2}$.
点评 本题考查了全等三角形的判定与性质,解直角三角形,平行四边形的性质,折叠的性质,勾股定理的应用,三角形面积等,熟练掌握平行四边形的性质,由勾股定理得出方程是解决问题的关键.

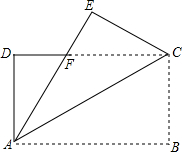 如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )
如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )| A. | 16cm | B. | 20cm | C. | 24cm | D. | 28cm |
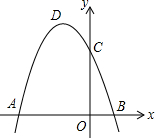 如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3).
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3).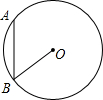 如图,AB是⊙O的弦,AB=6,OB=5,将线段AB向右侧平移,使之与圆相切,点B移至切点位置,则平移的距离为3$\sqrt{10}$.
如图,AB是⊙O的弦,AB=6,OB=5,将线段AB向右侧平移,使之与圆相切,点B移至切点位置,则平移的距离为3$\sqrt{10}$.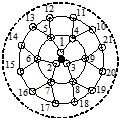 课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为150的微生物会出现在( )
课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为150的微生物会出现在( ) 解不等式:$\frac{x-1}{6}-\frac{x}{3}>-\frac{1}{2}$,并将解集在数轴上表示出来.
解不等式:$\frac{x-1}{6}-\frac{x}{3}>-\frac{1}{2}$,并将解集在数轴上表示出来.