题目内容
14. 如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是30.
(2)经过几秒,恰好使AM=2BN?
(3)经过几秒,点M、点N分别到原点O的距离相等?
分析 (1)根据点A表示的数为-10,OB=3OA,可得点B对应的数;
(2)①点N在点B左侧;②点N在点B右侧两种情况讨论求解;
(3)分①点M、点N在点O两侧;②点M、点N重合两种情况讨论求解.
解答 解:(1)OB=3OA=30.
故B对应的数是30,
故答案为:30;
(2)设经过y秒,恰好使AM=2BN.
①点N在点B左侧,则
3y=2(30-2y),
解得y=$\frac{60}{7}$,
2y=2×$\frac{60}{7}$=$\frac{120}{7}$<OB=30;
所以经过$\frac{60}{7}$秒时,AM=2BN;
②点N在点B右侧,则
3y=2(2y-30),
解得y=60,
2y=60×2=120>OB=30;
所以经过60秒时,AM=2BN.
综上所述,经过$\frac{60}{7}$或30秒,恰好使AM=2BN.
(3)设经过x秒,点M、点N分别到原点O的距离相等
①点M、点N在点O两侧,则
10-3x=2x,
解得x=2;
②点M、点N重合,则
3x-10=2x,
解得x=10.
所以经过2秒或10秒,点M、点N分别到原点O的距离相等.
点评 此题主要考查了一元一方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
9.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.如果单项式2xm+1y3与$\frac{1}{2}$x2yn是同类项,那么m、n的值分别为( )
| A. | m=2,n=3 | B. | m=1,n=2 | C. | m=1,n=3 | D. | m=2,n=2 |
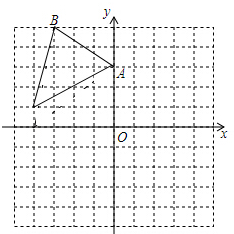 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(-3,5),C(-4,1).把△ABC向右平移2个单位,再向下平移3个单位得到△A1B1C1.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(-3,5),C(-4,1).把△ABC向右平移2个单位,再向下平移3个单位得到△A1B1C1.
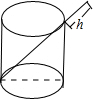 将一根26cm的筷子,置于底面直径为9cm,高12cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的最小值是11cm.
将一根26cm的筷子,置于底面直径为9cm,高12cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的最小值是11cm.