题目内容
5.若关于x的分式方程$\frac{x-m}{x-5}$=2有正数解,则m的取值范围是m<10且m≠5.分析 分式方程去分母转化为整式方程,求出整式方程的解表示出x,根据方程的解为正数,求出m的范围即可.
解答 解:分式方程去分母得:x-m=2(x-5),
解得:x=10-m,
∵关于x的分式方程$\frac{x-m}{x-5}$=2有正数解,
∴10-m>0,且x-5≠0,
解得:m<10,且m≠5.
故答案为:m<10且m≠5.
点评 此题考查了分式方程的解,解决本题的关键是熟记分数方程的解,注意在任何时候都要考虑分母不为0.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
16.下列三条线段能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,$\sqrt{2}$,2 | C. | $\sqrt{3}$,3,6 | D. | 6,8,10 |
20.若点C为线段Ab的黄金分割点,且AC>BC,则$\frac{BC}{AB}$的值为( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{3-\sqrt{5}}{2}$ | D. | $\sqrt{5}$-2 |
10.下列命题中,是真命题的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 若a⊥b,b⊥c则a⊥c | |
| C. | 同旁内角相等,两直线平行 | |
| D. | 若a∥b,b∥c,则a∥c |
 已知:如图,△ABC中,∠C=90°,∠B的平分线交AC于点D,CD=15,AD=25,求AB的长.
已知:如图,△ABC中,∠C=90°,∠B的平分线交AC于点D,CD=15,AD=25,求AB的长.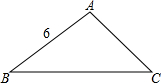 △ABC中,AB=6,∠B=30°,∠C=45°,求S△ABC(用含根式的式子表示)
△ABC中,AB=6,∠B=30°,∠C=45°,求S△ABC(用含根式的式子表示)