题目内容
14.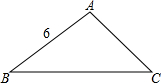 △ABC中,AB=6,∠B=30°,∠C=45°,求S△ABC(用含根式的式子表示)
△ABC中,AB=6,∠B=30°,∠C=45°,求S△ABC(用含根式的式子表示)
分析 作AD⊥BC于D,AD=CD,△ACD是等腰直角三角形;在直角△ABD中,根据∠B=30°,求出AD、BD、DC.从而求面积.
解答 解:作AD⊥BC于D,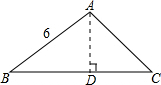
因为∠B=30°,AB=6,
所以AD=$\frac{1}{2}$AB=3,BD=3$\sqrt{3}$,
因为∠C=45°,
所以AD=CD=3,
所以S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×3(3+3$\sqrt{3}$)=$\frac{9}{2}$+$\frac{9\sqrt{3}}{2}$.
点评 本题考查了解直角三角形,一般的三角形的计算可以通过作高线,转化为直角三角形的问题求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.现已知线段AB=10,点P是线段AB的黄金分割点,PA>PB,那么线段PA的长约为( )
| A. | 6.18 | B. | 0.382 | C. | 0.618 | D. | 3.28 |
19.下列方程中是一元二次方程的是( )
| A. | x2+2x=3 | B. | x2+y=0 | C. | (x2-2)2=9 | D. | x+$\frac{1}{x}$=3 |
4.下面各式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{15}$ | B. | -$\sqrt{6}$ | C. | $\sqrt{8}$ | D. | 3$\sqrt{5}$ |
 解不等式组:$\left\{\begin{array}{l}{2x+1≥-1}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$.把解集在数轴上表示出来,并求出这个等式的整数解.
解不等式组:$\left\{\begin{array}{l}{2x+1≥-1}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$.把解集在数轴上表示出来,并求出这个等式的整数解.