题目内容
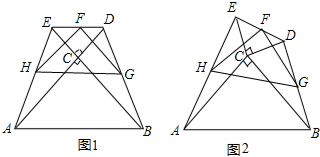
在图1、图2中,△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.
(1)如图1,点D、E分别在AC、BC的延长线上,求证:△FGH是等腰直角三角形;
(2)将图1中的△DEC绕点C顺时针旋转一个锐角,得到图2,△FGH还是等腰直角三角形吗?若是,请给出证明;若不是,请说明理由.
(1)如图1,点D、E分别在AC、BC的延长线上,求证:△FGH是等腰直角三角形;
(2)将图1中的△DEC绕点C顺时针旋转一个锐角,得到图2,△FGH还是等腰直角三角形吗?若是,请给出证明;若不是,请说明理由.

考点:全等三角形的判定与性质,等腰直角三角形,三角形中位线定理
专题:
分析:(1)由等腰三角形的性质可以得出CE=CD,CA=CB,进而求出AD=BE,由三角形中位线的性质可以求出HF=GF,∠HFG=90°,就可以求出结论;
(2)连结AD、BE,可以得出△ACD≌△BCE,就可以得出AD=BE,∠CAD=∠CBE,就可以得出∠BPQ=90°,进而求出∠GFH=90°而得出结论.
(2)连结AD、BE,可以得出△ACD≌△BCE,就可以得出AD=BE,∠CAD=∠CBE,就可以得出∠BPQ=90°,进而求出∠GFH=90°而得出结论.
解答:证明:(1)∵F是DE的中点,H是AE的中点,G是BD的中点,
∴HF,GF分别是△AED和△BED的中位线,
∴HF=
AD,GF=
BE,HF∥AD,GF∥BE,
∴∠FMC+∠DCE=180°,∠FNC+∠DCE=180°.
∵∠DCE=90°,
∴∠FMC=∠FNC=90°,
∴∠GFH=90°.
∵△ABC和△DEC都是等腰直角三角形,
∴AC=BC,EC=DC,
∴AC+DC=BC+EC,
即AD=BE.
∴HF=GF,
∴△FGH是等腰直角三角形;
(2)△FGH是等腰直角三角形.
理由:连结AD、BE,设AD交BE于点P,交BC于点Q,
∵△ABC和△DEC都是等腰直角三角形,
∴AC=BC,EC=DC.∠ACB=∠DCE=90°,
∴∠ACB+∠DCB=∠DCE+∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS)
∴AD=BE,∠CAD=∠CBE.
∵F是DE的中点,H是AE的中点,G是BD的中点,
∴HF,GF分别是△AED和△BED的中位线,
∴HF=
AD,GF=
BE,HF∥AD,GF∥BE,
∴HF=HF.
∵∠BQD+∠CBE=∠AQC+∠CAD=90°,
∴∠APB=90°.
同(1)可证∠HFG=90°,
∴△FGH是等腰直角三角形.
∴HF,GF分别是△AED和△BED的中位线,
∴HF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FMC+∠DCE=180°,∠FNC+∠DCE=180°.
∵∠DCE=90°,
∴∠FMC=∠FNC=90°,
∴∠GFH=90°.
∵△ABC和△DEC都是等腰直角三角形,
∴AC=BC,EC=DC,
∴AC+DC=BC+EC,
即AD=BE.
∴HF=GF,
∴△FGH是等腰直角三角形;

(2)△FGH是等腰直角三角形.
理由:连结AD、BE,设AD交BE于点P,交BC于点Q,
∵△ABC和△DEC都是等腰直角三角形,
∴AC=BC,EC=DC.∠ACB=∠DCE=90°,
∴∠ACB+∠DCB=∠DCE+∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS)
∴AD=BE,∠CAD=∠CBE.
∵F是DE的中点,H是AE的中点,G是BD的中点,
∴HF,GF分别是△AED和△BED的中位线,
∴HF=
| 1 |
| 2 |
| 1 |
| 2 |
∴HF=HF.
∵∠BQD+∠CBE=∠AQC+∠CAD=90°,
∴∠APB=90°.
同(1)可证∠HFG=90°,
∴△FGH是等腰直角三角形.
点评:本题考查了等腰直角三角形的性质的运用,三角形的中位线的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
已知点P为线段MN上一点,Q是NP的中点,若MQ=8,则MP+MN的值为( )
| A、12 | B、14 |
| C、16 | D、无法确定 |
 近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是12000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案:
近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是12000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案: 如图,点C为线段AB上一点,若线段AC=12cm,AC:CB=3:2,D、E两点分别为AC、AB的中点,求DE的长.
如图,点C为线段AB上一点,若线段AC=12cm,AC:CB=3:2,D、E两点分别为AC、AB的中点,求DE的长.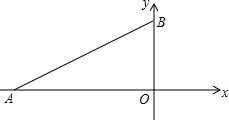 如图,在平面直角坐标系中,点A(-6,0),点B(0,2
如图,在平面直角坐标系中,点A(-6,0),点B(0,2 如图,直线AB、CD相交于O,且∠AOC:∠BOC=1:2,∠AOF=∠BOF=90°,OE平分∠BOC,求:∠EOF的度数.
如图,直线AB、CD相交于O,且∠AOC:∠BOC=1:2,∠AOF=∠BOF=90°,OE平分∠BOC,求:∠EOF的度数.


